
【題目】如圖,在四棱錐PABCD中,M是PA上的點,![]() 為正三角形,
為正三角形,![]() ,
,![]() .
.
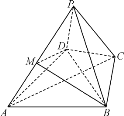
(1)求證:平面![]() 平面PAC;
平面PAC;
(2)若![]() ,
,![]() 平面BPC,求證:點M為線段PA的中點.
平面BPC,求證:點M為線段PA的中點.
【答案】(1)證明見解析;(2)證明見解析.
【解析】
(1)取BD的中點O,連結OA,OC,可證![]() ,又由
,又由![]() ,可得
,可得![]() 平面PAC,即可得證;
平面PAC,即可得證;
(2)取AB的中點N,連結MN和DN,首先可得![]() ,
,![]() ,所以
,所以![]() ,即可得到
,即可得到![]() 平面BPC.又由
平面BPC.又由![]() 平面BPC,可得平面
平面BPC,可得平面![]() 平面BPC.根據面面平行的性質可得
平面BPC.根據面面平行的性質可得![]() ,即可得證;
,即可得證;
(1)取BD的中點O,連結OA,OC,
∵![]() 為正三角形,∴
為正三角形,∴![]() .
.
∵![]() ,∴
,∴![]() .
.
在平面![]() 內,過O點垂直于BD的直線有且只有一條,
內,過O點垂直于BD的直線有且只有一條,
∴A,O,C三點共線,即![]() .
.
∵![]() ,AC,
,AC,![]() 平面PAC,
平面PAC,![]() ,
,
∴![]() 平面PAC.∵
平面PAC.∵![]() 平面MBD,
平面MBD,
∴平面![]() 平面PAC.
平面PAC.
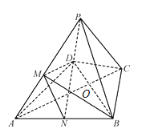
(2)取AB的中點N,連結MN和DN,
因為![]() ,且
,且![]() ,所以
,所以![]()
所以![]() ,即
,即![]() .
.
∵![]() 為正三角形,∴
為正三角形,∴![]() .
.
又DN,BC,AB共面,∴![]() .
.
∵![]() 平面BPC,
平面BPC,![]() 平面BPC,
平面BPC,
∴![]() 平面BPC.
平面BPC.
∵![]() 平面BPC,DN,
平面BPC,DN,![]() 平面DMN,
平面DMN,
∴平面![]() 平面BPC.
平面BPC.
∵![]() 平面DMN,∴
平面DMN,∴![]() 平面BPC.
平面BPC.
∵![]() 平面PAB,平面
平面PAB,平面![]() 平面BPC=PB,
平面BPC=PB,
∴![]() .
.
∵N是AB的中點,∴M為線段PA的中點.


 通城學典默寫能手系列答案
通城學典默寫能手系列答案 金牌教輔培優優選卷期末沖刺100分系列答案
金牌教輔培優優選卷期末沖刺100分系列答案科目:高中數學 來源: 題型:
【題目】下列4個說法中正確的有( )
①命題“若![]() ,則
,則![]() ”的逆否命題為“若
”的逆否命題為“若![]() 則
則![]() ”;
”;
②若![]() ,則
,則![]() ;
;
③若復合命題:“![]() ”為假命題,則p,q均為假命題;
”為假命題,則p,q均為假命題;
④“![]() ”是“
”是“![]() ”的充分不必要條件.
”的充分不必要條件.
A.①②③B.②③④C.①②④D.①③④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 為等差數列,
為等差數列,![]() ,
,![]() ,
,![]() 分別是下表第一、二、三行中的某一個數,且
分別是下表第一、二、三行中的某一個數,且![]() ,
,![]() ,
,![]() 中的任何兩個數都不在下表的同一列.
中的任何兩個數都不在下表的同一列.
第一列 | 第二列 | 第三列 | |
第一行 | |||
第二行 | 4 | 6 | 9 |
第三行 | 12 | 8 | 7 |
請從①![]() ,②
,②![]() ,③
,③ ![]() 的三個條件中選一個填入上表,使滿足以上條件的數列
的三個條件中選一個填入上表,使滿足以上條件的數列![]() 存在;并在此存在的數列
存在;并在此存在的數列![]() 中,試解答下列兩個問題
中,試解答下列兩個問題
(1)求數列![]() 的通項公式;
的通項公式;
(2)設數列![]() 滿足
滿足![]() ,求數列
,求數列![]() 的前n項和
的前n項和![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學校實行新課程改革,即除語、數、外三科為必考科目外,還要在理、化、生、史、地、政六科中選擇三科作為選考科目.已知某生的高考志愿為某大學環境科學專業,按照該大學上一年高考招生選考科目要求理、化必選,為該生安排課表(上午四節、下午四節,每門課每天至少一節),已知該生某天最后兩節為自習課,且數學不排下午第一節,語文、外語不相鄰(上午第四節和下午第一節不算相鄰),則該生該天課表有( ).
A.444種B.1776種C.1440種D.1560種
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為![]() 為參數),在以坐標原點
為參數),在以坐標原點![]() 為極點,
為極點,![]() 軸的正半軸為極軸的極坐標系中,點
軸的正半軸為極軸的極坐標系中,點![]() 的極坐標為
的極坐標為![]() ,直線
,直線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求直線![]() 的直角坐標方程與曲線
的直角坐標方程與曲線![]() 的普通方程;
的普通方程;
(2)若![]() 是曲線
是曲線![]() 上的動點,
上的動點,![]() 為線段
為線段![]() 的中點,求點
的中點,求點![]() 到直線
到直線![]() 的距離的最大值.
的距離的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線![]() ,拋物線上的點
,拋物線上的點![]() 到焦點的距離為2.
到焦點的距離為2.
(1)求拋物線的方程和![]() 的值;
的值;
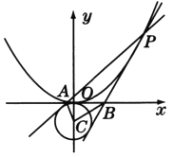
(2)如圖,![]() 是拋物線上的一點,過
是拋物線上的一點,過![]() 作圓
作圓![]() 的兩條切線交
的兩條切線交![]() 軸于
軸于![]() ,
,![]() 兩點,若
兩點,若![]() 的面積為
的面積為![]() ,求點
,求點![]() 的坐標.
的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com