
【題目】如圖,設![]() ,
,![]() 分別是正方體
分別是正方體![]() 的棱
的棱![]() 上兩點,且
上兩點,且![]() ,
,![]() ,其中正確的命題為( )
,其中正確的命題為( )
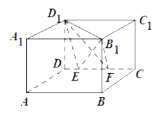
A.三棱錐![]() 的體積為定值
的體積為定值
B.異面直線![]() 與
與![]() 所成的角為
所成的角為![]()
C.![]() 平面
平面![]()
D.直線![]() 與平面
與平面![]() 所成的角為
所成的角為![]()
【答案】AD
【解析】
A. 利用![]() ,三棱錐
,三棱錐![]() 的體積為定值,正確
的體積為定值,正確
B. 利用平移法找異面直線所成的角,![]() ,
,![]() 和
和![]() 所成的角為
所成的角為![]() ,所以異面直線
,所以異面直線![]() 與
與![]() 所成的角為
所成的角為![]() ,故B錯誤
,故B錯誤
C. 若![]() 平面
平面![]() ,則線
,則線![]() 與
與![]() 所成的角為
所成的角為![]() ,而異面直線
,而異面直線![]() 與
與![]() 所成的角為
所成的角為![]() ,故C錯誤
,故C錯誤
D,建立坐標系,用向量坐標法求解,先求出平面![]() 的一個法向量,再求平面
的一個法向量,再求平面![]() 的一個法向量和
的一個法向量和![]() 的方向向量的夾角,正確
的方向向量的夾角,正確
解:對于A,

故三棱錐![]() 的體積為定值,故A正確
的體積為定值,故A正確
對于B, ![]() ,
,![]() 和
和![]() 所成的角為
所成的角為![]() ,異面直線
,異面直線![]() 與
與![]() 所成的角為
所成的角為![]() ,故B錯誤
,故B錯誤
對于C, 若![]() 平面
平面![]() ,則
,則![]() 直線
直線![]() ,即異面直線
,即異面直線![]() 與
與![]() 所成的角為
所成的角為![]() ,故C錯誤
,故C錯誤
對于D,以![]() 為坐標原點,分布以
為坐標原點,分布以![]() 為
為![]() 軸,
軸,![]() 軸,
軸,![]() 軸,建立空間直角坐標系,設
軸,建立空間直角坐標系,設![]() ,則
,則![]() ,
,![]() ,
,![]()
![]()
設平面![]() 的法向量為
的法向量為![]() 則
則
 ,即
,即![]()
令![]() ,則
,則![]()
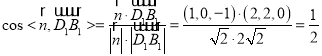
![]()
所以直線![]() 與平面
與平面![]() 所成的角為
所成的角為![]() ,正確
,正確
故選:AD


 期末沖刺100分創新金卷完全試卷系列答案
期末沖刺100分創新金卷完全試卷系列答案科目:高中數學 來源: 題型:
【題目】已知橢圓C:![]() 的離心率為
的離心率為![]() ,點P
,點P![]() 在C上.
在C上.
(1)求橢圓C的方程;
(2)設![]() 分別為橢圓C的左右焦點,過
分別為橢圓C的左右焦點,過![]() 的直線
的直線![]() 與橢圓C交于不同的兩點A、B,求△
與橢圓C交于不同的兩點A、B,求△![]() 的內切圓的半徑的最大值.
的內切圓的半徑的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】根據中國生態環境部公布的2017年、2018年長江流域水質情況監測數據,得到如下餅圖:
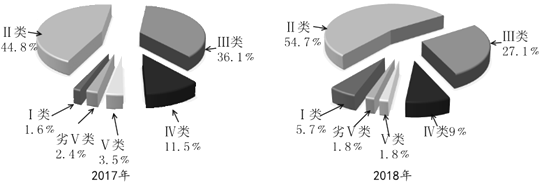
則下列說法錯誤的是( )
A.2018年的水質情況好于2017年的水質情況
B.2018年與2017年相比較,Ⅰ、Ⅱ類水質的占比明顯增加
C.2018年與2017年相比較,占比減小幅度最大的是Ⅳ類水質
D.2018年Ⅰ、Ⅱ類水質的占比超過![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() (
(![]() ,
,![]() ),且
),且![]() 的解集為
的解集為![]() ;數列
;數列![]() 的前
的前![]() 項和為
項和為![]() ,對任意
,對任意![]() ,滿足
,滿足![]() .
.
(1)求![]() 的值及數列
的值及數列![]() 的通項公式;
的通項公式;
(2)已知數列![]() 的前
的前![]() 項和為
項和為![]() ,滿足
,滿足![]() ,
,![]() ,求數列
,求數列![]() 的前
的前![]() 項和
項和![]() ;
;
(3)已知數列![]() 滿足
滿足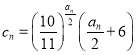 ,若
,若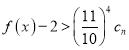 對
對![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙兩人2013-2017這五年的年度體檢的血壓值的折線圖如圖所示.

(1)根據散點圖,直接判斷甲、乙這五年年度體檢的血壓值誰的波動更大,并求波動更大者的方差;
(2)根據乙這五年年度體檢血壓值的數據,求年度體檢血壓值![]() 關于年份
關于年份![]() 的線性回歸方程,并據此估計乙在2018年年度體檢的血壓值.
的線性回歸方程,并據此估計乙在2018年年度體檢的血壓值.
(附: ,
,![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一個口袋內裝有大小相同的7個白球和1個黑球.
(1)從口袋內取出3個球,共有多少種取法?
(2)從口袋內取出3個球,使其中含有1個黑球,有多少種取法?
(3)從口袋內取出3個球,使其中不含黑球,有多少種取法?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列命題錯誤的是
A. 三棱錐的四個面可以都是直角三角形;
B. 等差數列{an}的前n項和為Sn(n=1,2,3…),若當首項a1和公差d變化時,a5+a8+a11是一個定值,則S16為定值;
C. ![]() 中,sinA>sinB是
中,sinA>sinB是![]() 的充要條件;
的充要條件;
D. 若雙曲線的漸近線互相垂直,則這條雙曲線是等軸雙曲線.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com