
【題目】已知函數![]() 對一切實數
對一切實數![]() 都有
都有![]()
![]() 成立,且
成立,且![]() .
.
(1)求![]() 的值;
的值;
(2)求![]() 的解析式;
的解析式;
(3)已知![]() ,設
,設![]() :當
:當![]() 時,不等式
時,不等式![]() 恒成立;Q:當
恒成立;Q:當![]() 時,
時,![]() 是單調函數。如果滿足
是單調函數。如果滿足![]() 成立的
成立的![]() 的集合記為
的集合記為![]() ,滿足Q成立的
,滿足Q成立的![]() 的集合記為
的集合記為![]() ,求A∩(CRB)(
,求A∩(CRB)(![]() 為全集).
為全集).
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】試題分析:(1)對抽象函數滿足的函數值關系的理解和把握是解決該問題的關鍵,對自變量適當的賦值可以解決該問題,結合已知條件可以賦![]() 求出
求出![]() ;(2)在(1)基礎上賦值
;(2)在(1)基礎上賦值![]() 可以實現求解
可以實現求解![]() 的解析式的問題;(3)利用(2)中求得的函數的解析式,結合恒成立問題的求解策略,即轉化為相應的二次函數最值問題求出集合
的解析式的問題;(3)利用(2)中求得的函數的解析式,結合恒成立問題的求解策略,即轉化為相應的二次函數最值問題求出集合![]() ,利用二次函數的單調性求解策略求出集合
,利用二次函數的單調性求解策略求出集合![]() .
.
試題解析:(1)令x=﹣1,y=1,則由已知f(0)﹣f(1)=﹣1(﹣1+2+1)
∴f(0)=﹣2
(2)令y=0,則f(x)﹣f(0)=x(x+1)
又∵f(0)=﹣2,∴f(x)=x2+x﹣2
(3)不等式f(x)+3<2x+a即x2+x﹣2+3<2x+a
也就是x2﹣x+1<a.由于當![]() 時,
時,![]() ,
,
又x2﹣x+1=![]() 恒成立,
恒成立,
故A={a|a≥1},g(x)=x2+x﹣2﹣ax=x2+(1﹣a)x﹣2 對稱軸x=![]() ,
,
又g(x)在[﹣2,2]上是單調函數,故有![]() ,或
,或![]() ,
,
∴B={a|a≤﹣3,或a≥5},CRB={a|﹣3<a<5},∴A∩CRB={a|1≤a<5}.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
極坐標系的極點為直角坐標系![]() 的原點,極軸為
的原點,極軸為![]() 軸的正半軸,兩種坐標系中的長度單位相同,已知曲線
軸的正半軸,兩種坐標系中的長度單位相同,已知曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求![]() 的直角坐標方程;
的直角坐標方程;
(2)直線 (
(![]() 為參數)與曲線
為參數)與曲線![]() 交于
交于![]() 兩點,與
兩點,與![]() 軸交于
軸交于![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《中華人民共和國個人所得稅》規定,公民月工資、薪金所得不超過3500元的部分不納稅,超過3500元的部分為全月納稅所得額,此項稅款按下表分段累計計算:

已知張先生的月工資、薪金所得為10000元,問他當月應繳納多少個人所得稅?
設王先生的月工資、薪金所得為![]() 元,當月應繳納個人所得稅為
元,當月應繳納個人所得稅為![]() 元,寫出
元,寫出![]() 與
與![]() 的函數關系式;
的函數關系式;
(3)已知王先生一月份應繳納個人所得稅為303元,那么他當月的個工資、薪金所得為多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖(1)所示,E為矩形ABCD的邊AD上一點,動點P、Q同時從點B出發,點P以1cm/秒的速度沿折線BE-ED-DC運動到點C時停止,點Q以2cm/秒的速度沿BC運動到點C時停止.設P、Q同時出發t秒時,△BPQ的面積為ycm2.已知y與t的函數關系圖象如圖(2)(其中曲線OG為拋物線的一部分,其余各部分均為線段),則下列結論:①![]() ;②當
;②當![]() 時,
時, ![]() ;③
;③![]() ;④當
;④當![]() 秒時,
秒時, ![]() ∽
∽![]() ;⑤當
;⑤當![]() 的面積為
的面積為![]() 時,時間
時,時間![]() 的值是
的值是![]() 或
或![]() ;其中正確的結論是( )
;其中正確的結論是( )
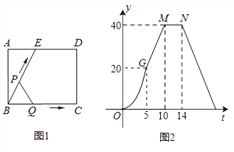
A. ①⑤ B. ②⑤ C. ②③ D. ②④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知如圖,圓![]() 、橢圓
、橢圓![]() 均經過點M
均經過點M![]() ,圓
,圓![]() 的圓心為
的圓心為![]() ,橢圓
,橢圓![]() 的兩焦點分別為
的兩焦點分別為![]() .
.
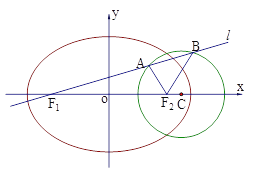
(Ⅰ)分別求圓![]() 和橢圓
和橢圓![]() 的標準方程;
的標準方程;
(Ⅱ)過![]() 作直線
作直線![]() 與圓
與圓![]() 交于
交于![]() 、
、![]() 兩點,試探究
兩點,試探究![]() 是否為定值?若是定值,求出該定值;若不是,說明理由.
是否為定值?若是定值,求出該定值;若不是,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某高職院校進行自主招生文化素質考試,考試內容為語文、數學、英語三科,總分為200分.現從上線的考生中隨機抽取20人,將其成績用莖葉圖記錄如下:
男 | 女 | |||||||||||
15 | 6 | |||||||||||
5 | 4 | 16 | 3 | 5 | 8 | |||||||
8 | 2 | 17 | 2 | 3 | 6 | 8 | 8 | 8 | ||||
6 | 5 | 18 | 5 | 7 | ||||||||
19 | 2 | 3 | ||||||||||
(Ⅰ)計算上線考生中抽取的男生成績的方差![]() ;(結果精確到小數點后一位)
;(結果精確到小數點后一位)
(Ⅱ)從上述莖葉圖180分以上的考生中任選2人作為考生代表出席座談會,求所選考生恰為一男一女的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若函數f(x)滿足f(logax)=![]() ·(x-
·(x-![]() )(其中a>0且a≠1).
)(其中a>0且a≠1).
(1)求函數f(x)的解析式,并判斷其奇偶性和單調性;
(2)當x∈(-∞,2)時,f(x)-4的值恒為負數,求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】共享單車是城市慢行系統的一種模式創新,對于解決民眾出行“最后一公里”的問題特別見效,由于停取方便、租用價格低廉,各色共享單車受到人們的熱捧.某自行車廠為共享單車公司生產新樣式的單車,已知生產新樣式單車的固定成本為20000元,每生產一件新樣式單車需要增加投入100元.根據初步測算,自行車廠的總收益(單位:元)滿足分段函數![]() ,其中
,其中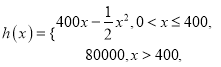
![]() 是新樣式單車的月產量(單位:件),利潤
是新樣式單車的月產量(單位:件),利潤![]() 總收益
總收益![]() 總成本.
總成本.
(1)試將自行車廠的利潤![]() 元表示為月產量
元表示為月產量![]() 的函數;
的函數;
(2)當月產量為多少件時自行車廠的利潤最大?最大利潤是多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com