
【題目】已知圓C的極坐標方程為 ![]() ,直線l的參數(shù)方程為
,直線l的參數(shù)方程為 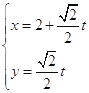 (t為常數(shù),t∈R)
(t為常數(shù),t∈R)
(1)求直線l的普通方程和圓C的直角坐標方程;
(2)求直線l與圓C相交的弦長.
 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:高中數(shù)學 來源: 題型:
【題目】已知f(x)= ![]() ,其中
,其中 ![]() =(2cosx,﹣
=(2cosx,﹣ ![]() sin2x),
sin2x), ![]() =(cosx,1),x∈R.
=(cosx,1),x∈R.
(1)求f(x)的周期及單調遞增區(qū)間;
(2)在△ABC中,角A,B,C所對的邊分別為a,b,c,f(A)=﹣1,a= ![]() ,且向量
,且向量 ![]() 與
與 ![]() 共線,求邊長b和c的值.
共線,求邊長b和c的值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某次數(shù)學測驗共有10道選擇題,每道題共有四個選項,且其中只有一個選項是正確的,評分標準規(guī)定:每選對1道題得5分,不選或選錯得0分,某考試每道都選并能確定其中有6道題能選對,其余4道題無法確定正確選項,但這4道題中有2道能排除兩個錯誤選項,另2題只能排除一個錯誤選項,于是該生做這4道題時每道題都從不能排除的選項中隨機挑選一個選項做答,且各題做答互不影響.
(Ⅰ)求該考生本次測驗選擇題得50分的概率;
(Ⅱ)求該考生本次測驗選擇題所得分數(shù)的分布列和數(shù)學期望.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知圓錐曲線![]() (
( ![]() 為參數(shù))和定點
為參數(shù))和定點![]() , F1 、 F2 是此圓錐曲線的左、右焦點,以原點 O 為極點,以 x 軸的正半軸為極軸建立極坐標系.
, F1 、 F2 是此圓錐曲線的左、右焦點,以原點 O 為極點,以 x 軸的正半軸為極軸建立極坐標系.
(1)求直線 AF2 的直角坐標方程;
(2)經(jīng)過點 F1 且與直線AF2 垂直的直線 l 交此圓錐曲線于M,N 兩點,求||MF1|-|NF1|| 的值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】若二次函數(shù) ![]() 的圖象和直線y=x無交點,現(xiàn)有下列結論:
的圖象和直線y=x無交點,現(xiàn)有下列結論:
①方程f[f(x)]=x一定沒有實數(shù)根;
②若a>0,則不等式f[f(x)]>x對一切實數(shù)x都成立;
③若a<0,則必存存在實數(shù)x0 , 使f[f(x0)]>x0;
④若a+b+c=0,則不等式f[f(x)]<x對一切實數(shù)都成立;
⑤函數(shù) ![]() 的圖象與直線y=﹣x也一定沒有交點.
的圖象與直線y=﹣x也一定沒有交點.
其中正確的結論是(寫出所有正確結論的編號).
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知曲線 ![]() 的參數(shù)方程是
的參數(shù)方程是 ![]() ,直線
,直線 ![]() 的參數(shù)方程為
的參數(shù)方程為  ,
,
(1)求曲線 ![]() 與直線
與直線 ![]() 的普通方程;
的普通方程;
(2)若直線 ![]() 與曲線
與曲線 ![]() 相交于
相交于 ![]() 兩點,且
兩點,且 ![]() ,求實數(shù)
,求實數(shù) ![]() 的值
的值
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】對于函數(shù)f(x)的定義域中任意的x1、x2(x1≠x2),有如下結論:
①f(x1+x2)=f(x1)f(x2);
②f(x1x2)=f(x1)+f(x2);
③ ![]() >0;
>0;
④f( ![]() )<
)< ![]() .
.
當f(x)=2x時,上述結論中正確的有( )個.
A.3
B.2
C.1
D.0
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某校在高二年級開展了體育分項教學活動,將體育課分為大球(包括籃球、排球、足球)、小球(包括乒乓球、羽毛球)、田徑、體操四大項(以下簡稱四大項,并且按照這個順序).為體現(xiàn)公平,學校規(guī)定時間讓學生在電腦上選課,據(jù)初步統(tǒng)計,在全年級980名同學中,有意申報四大項的人數(shù)之比為3:2:1:1,而實際上由于受多方面條件影響,最終確定的四大項人數(shù)必須控制在2:1:3:1,選課不成功的同學由電腦自動調劑到田徑類.
(Ⅰ)隨機抽取一名同學,求該同學選課成功(未被調劑)的概率;
(Ⅱ)某小組有五名同學,有意申報四大項的人數(shù)分別為2、1、1、1,記最終確定到田徑類的人數(shù)為![]() ,求
,求![]() 的分布列及數(shù)學期望
的分布列及數(shù)學期望![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某保險公司利用簡單隨機抽樣方法,對投保車輛進行抽樣,樣本車輛中每輛車的賠付結果統(tǒng)計如下:
賠付金額(元) | 0 | 1 000 | 2 000 | 3 000 | 4 000 |
車輛數(shù)(輛) | 500 | 130 | 100 | 150 | 120 |
(1)若每輛車的投保金額均為2800元,估計賠付金額大于投保金額的概率.
(2)在樣本車輛中,車主是新司機的占10%,在賠付金額為4000元的樣本車輛中,車主是新司機的占20%,估計在已投保車輛中,新司機獲賠金額為4000元的概率.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com