
【題目】設函數![]() .
.
(![]() )求不等式
)求不等式![]() 的解集.
的解集.
(![]() )若對于
)若對于![]() ,
, ![]() 恒成立,求
恒成立,求![]() 的取值范圍.
的取值范圍.
【答案】(1)當![]() 時,解集為
時,解集為![]() ;當
;當![]() 時,解集為
時,解集為![]() ,當
,當![]() 時,解集為
時,解集為![]() ;(2)
;(2)![]() .
.
【解析】試題分析:(1)不等式![]() 等價于
等價于![]() ,分三種情況討論,當
,分三種情況討論,當![]() 時,當
時,當![]() 時,當
時,當![]() 時,分別利用一元二次不等式的解法求解即可;(2)對任意的
時,分別利用一元二次不等式的解法求解即可;(2)對任意的![]() ,
, ![]() 恒成立,等價于
恒成立,等價于![]() ,設
,設![]() ,則
,則![]() 在
在![]() 上單調減,
上單調減, ![]() ,從而可得
,從而可得![]() ,
, ![]() .
.
試題解析:(![]() )解:∵
)解:∵![]() ,∴
,∴![]()
![]() ,當
,當![]() 時,解為:
時,解為: ![]() ,當
,當![]() 時,解為:
時,解為: ![]() ,當
,當![]() 時,解為:
時,解為: ![]() ,綜上:當
,綜上:當![]() 時,解集為
時,解集為![]() ;當
;當![]() 時,解集為
時,解集為![]() ,當
,當![]() 時,解集為
時,解集為![]() .
.
(![]() )∵對任意的
)∵對任意的![]() ,
, ![]() 恒成立,
恒成立, ![]()
![]()
![]() ,設:
,設: ![]() ,則
,則![]() 在
在![]() 上單調減,
上單調減,
則: ![]() ,∴
,∴![]() ,
, ![]() .
.
【方法點晴】本題主要考查一元二次不等式的解法以及不等式恒成立問題、分類討論思想的應用,屬于中檔題.不等式恒成立問題常見方法:① 分離參數![]() 恒成立(
恒成立(![]() 即可)或
即可)或![]() 恒成立(
恒成立(![]() 即可);② 數形結合(
即可);② 數形結合(![]() 圖象在
圖象在![]() 上方即可);③ 討論最值
上方即可);③ 討論最值![]() 或
或![]() 恒成立;④ 討論參數.本題是利用方法 ① 求得
恒成立;④ 討論參數.本題是利用方法 ① 求得![]() 的取值范圍.
的取值范圍.


 互動課堂系列答案
互動課堂系列答案 激活思維智能訓練課時導學練系列答案
激活思維智能訓練課時導學練系列答案科目:高中數學 來源: 題型:
【題目】對于數列![]() ,設
,設![]() 表示數列
表示數列![]() 前
前![]() 項
項![]() ,
, ![]() ,
, ![]() ,
, ![]() 中的最大項.數列
中的最大項.數列![]() 滿足:
滿足: ![]() .
.
(![]() )若
)若![]() ,求
,求![]() 的前
的前![]() 項和.
項和.
(![]() )設數列
)設數列![]() 為等差數列,證明:
為等差數列,證明: ![]() 或者
或者![]() (
(![]() 為常數),
為常數),![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
(![]() )設數列
)設數列![]() 為等差數列,公差為
為等差數列,公差為![]() ,且
,且![]() .
.
記![]() ,
,
求證:數列![]() 是等差數列.
是等差數列.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設集合A={x|4x﹣1|<9,x∈R},B={x| ![]() ≥0,x∈R},則(RA)∩B=( )
≥0,x∈R},則(RA)∩B=( )
A.(﹣∞,﹣3)∪[ ![]() ,+∞)
,+∞)
B.(﹣3,﹣2]∪[0, ![]() )??
)??
C.(﹣∞,﹣3]∪[ ![]() ,+∞)
,+∞)
D.(﹣3,﹣2]
查看答案和解析>>
科目:高中數學 來源: 題型:
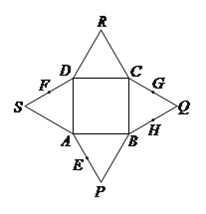
【題目】如圖,已知四邊形![]() 是正方形,
是正方形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 都是等邊三角形,
都是等邊三角形, ![]() 、
、![]() 、
、![]() 、
、![]() 分別是線段
分別是線段![]() 、
、![]() 、
、![]() 、
、![]() 的中點,分別以
的中點,分別以![]() 、
、![]() 、
、![]() 、
、![]() 為折痕將四個等邊三角形折起,使得
為折痕將四個等邊三角形折起,使得![]() 、
、![]() 、
、![]() 、
、![]() 四點重合于一點
四點重合于一點![]() ,得到一個四棱錐.對于下面四個結論:
,得到一個四棱錐.對于下面四個結論:
①![]() 與
與![]() 為異面直線; ②直線
為異面直線; ②直線![]() 與直線
與直線![]() 所成的角為
所成的角為![]()
③![]() 平面
平面![]() ; ④平面
; ④平面![]() 平面
平面![]() ;
;
其中正確結論的個數有( )
A. ![]() 個 B.
個 B. ![]() 個 C.
個 C. ![]() 個 D.
個 D. ![]() 個
個
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,已知圓
中,已知圓![]() 的方程為:
的方程為: ![]() ,直線
,直線![]() 的方程為
的方程為![]() .
.
(![]() )當
)當![]() 時,求直線
時,求直線![]() 被圓
被圓![]() 截得的弦長;
截得的弦長;
(![]() )當直線
)當直線![]() 被圓
被圓![]() 截得的弦長最短時,求直線
截得的弦長最短時,求直線![]() 的方程;
的方程;
(![]() )在(
)在(![]() )的前提下,若
)的前提下,若![]() 為直線
為直線![]() 上的動點,且圓
上的動點,且圓![]() 上存在兩個不同的點到點
上存在兩個不同的點到點![]() 的距離為
的距離為![]() ,求點
,求點![]() 的橫坐標的取值范圍.
的橫坐標的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C: ![]() =1(a>b>0)過點(
=1(a>b>0)過點( ![]() ,1),且以橢圓短軸的兩個端點和一個焦點為頂點的三角形是等腰直角三角形.
,1),且以橢圓短軸的兩個端點和一個焦點為頂點的三角形是等腰直角三角形.
(1)求橢圓的標準方程;
(2)設M(x,y)是橢圓C上的動點,P(p,0)是x軸上的定點,求|MP|的最小值及取最小值時點M的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com