
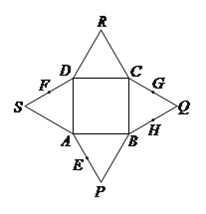
【題目】如圖,已知四邊形![]() 是正方形,
是正方形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 都是等邊三角形,
都是等邊三角形, ![]() 、
、![]() 、
、![]() 、
、![]() 分別是線段
分別是線段![]() 、
、![]() 、
、![]() 、
、![]() 的中點,分別以
的中點,分別以![]() 、
、![]() 、
、![]() 、
、![]() 為折痕將四個等邊三角形折起,使得
為折痕將四個等邊三角形折起,使得![]() 、
、![]() 、
、![]() 、
、![]() 四點重合于一點
四點重合于一點![]() ,得到一個四棱錐.對于下面四個結論:
,得到一個四棱錐.對于下面四個結論:
①![]() 與
與![]() 為異面直線; ②直線
為異面直線; ②直線![]() 與直線
與直線![]() 所成的角為
所成的角為![]()
③![]() 平面
平面![]() ; ④平面
; ④平面![]() 平面
平面![]() ;
;
其中正確結論的個數有( )
A. ![]() 個 B.
個 B. ![]() 個 C.
個 C. ![]() 個 D.
個 D. ![]() 個
個
【答案】D
【解析】①錯誤.所得四棱錐中,設![]() 中點為
中點為![]() ,則
,則![]() 、
、![]() 兩點重合,∵
兩點重合,∵![]() ,即
,即![]() ,即
,即![]() 與
與![]() 不是異面直線;②正確.∵
不是異面直線;②正確.∵![]() ,
, ![]() 與
與![]() 重合,且
重合,且![]() 與
與![]() 所成角為
所成角為![]() ,說明
,說明![]() 與
與![]() 所成角為
所成角為![]() ;③正確.∵
;③正確.∵![]() ,
, ![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() ;④正確.∵
;④正確.∵![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
, ![]() 點,∴平面
點,∴平面![]() 平面
平面![]() ,即平面
,即平面![]() 平面
平面![]() ,故選
,故選![]() .
.
【 方法點睛】本題主要通過對多個命題真假的判斷,主要綜合考查線線成角、線面成角、線面平行以及面面平行的判斷,屬于難題.這種題型綜合性較強,也是高考的命題熱點,同學們往往因為某一處知識點掌握不好而導致“全盤皆輸”,因此做這類題目更要細心、多讀題,盡量挖掘出題目中的隱含條件,另外,要注意從簡單的自己已經掌握的知識點入手,然后集中精力突破較難的命題.


 高效智能課時作業系列答案
高效智能課時作業系列答案 捷徑訓練檢測卷系列答案
捷徑訓練檢測卷系列答案科目:高中數學 來源: 題型:
【題目】數列{an}滿足a1=2,an+1=an2+6an+6(n∈N×)
(1)設Cn=log5(an+3),求證{Cn}是等比數列;
(2)求數列{an}的通項公式;
(3)設bn= ![]() ﹣
﹣ ![]() ,數列{bn}的前n項和為Tn , 求證:﹣
,數列{bn}的前n項和為Tn , 求證:﹣ ![]() ≤Tn<﹣
≤Tn<﹣ ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓C的圓心在直線3x+y﹣1=0上,且圓C在x軸、y軸上截得的弦長AB和MN分別為 ![]() 和
和 ![]() .
.
(1)求圓C的方程;
(2)若圓心C位于第四象限,點P(x,y)是圓C內一動點,且x,y滿足 ![]() ,求
,求 ![]() 的范圍.
的范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知△ABC中,角A、B、C的對邊分別為a、b、c,已知a=2,A=45°,若三角形有兩解,則邊b的取值范圍是( )
A.b>2
B.b<2
C.2<b<2 ![]()
D.2<b<2 ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在△ABC中,∠BAC=90°,D是BC邊的中點,AE⊥AD,AE交CB的延長線于E,則下面結論中正確的是( )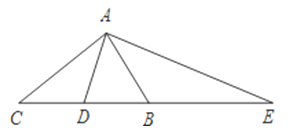
A.△AED∽△ACB
B.△AEB∽△ACD
C.△BAE∽△ACE
D.△AEC∽△DAC
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在直角坐標系 ![]() 中,直線 的參數方程為
中,直線 的參數方程為  (
( ![]() 為參數),以原點為極點,
為參數),以原點為極點, ![]() 軸正半軸為極軸建立極坐標系,圓
軸正半軸為極軸建立極坐標系,圓 ![]() 的極坐標方程為
的極坐標方程為 ![]() .
.
(1)寫出圓 ![]() 的直角坐標方程;
的直角坐標方程;
(2)![]() 為直線
為直線 ![]() 上一動點,當
上一動點,當 ![]() 到圓心
到圓心 ![]() 的距離最小時,求
的距離最小時,求 ![]() 的直角坐標.
的直角坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設![]() 是公差不為零的等差數列,滿足
是公差不為零的等差數列,滿足![]() 數列
數列![]() 的通項公式為
的通項公式為![]()
(1)求數列![]() 的通項公式;
的通項公式;
(2)將數列![]() ,
,![]() 中的公共項按從小到大的順序構成數列
中的公共項按從小到大的順序構成數列![]() ,請直接寫出數列
,請直接寫出數列![]() 的通項公式;
的通項公式;
(3)記![]() ,是否存在正整數
,是否存在正整數![]()
![]() ,使得
,使得![]() 成等差數列?若存在,求出
成等差數列?若存在,求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com