
【題目】設函數![]() ,
,![]() .
.
(1)討論![]() 在
在![]() 上的單調性;
上的單調性;
(2)當![]() 時,若存在正實數
時,若存在正實數![]() ,使得對
,使得對![]() ,都有
,都有![]() ,求
,求![]() 的取值范圍..
的取值范圍..
【答案】(1)見解析;(2)![]() .
.
【解析】
(1)求得![]() ,然后分
,然后分![]() 和
和![]() 兩種情況討論,分析導數在區間
兩種情況討論,分析導數在區間![]() 上的符號變化,即可得出函數
上的符號變化,即可得出函數![]() 在區間
在區間![]() 上的單調區間;
上的單調區間;
(2)由(1)可知,當![]() 時,函數
時,函數![]() 在
在![]() 上單調遞減,則
上單調遞減,則![]() ,使得對任意
,使得對任意![]() ,都有
,都有![]() ,構造函數
,構造函數![]() ,分
,分![]() 和
和![]() 兩種情況討論,分析函數
兩種情況討論,分析函數![]() 的單調性,結合
的單調性,結合![]() 在區間
在區間![]() 上恒成立可求得實數
上恒成立可求得實數![]() 的取值范圍.
的取值范圍.
(1)由![]() ,得
,得![]() ,
,![]() ,
,![]() ,
,
當![]() 時,由
時,由![]() ,得
,得![]() ,即函數
,即函數![]() 在
在![]() 上單調遞增,
上單調遞增,
由![]() ,得
,得![]() ,即函數
,即函數![]() 在
在![]() 上單調遞減;
上單調遞減;
當![]() 時,
時,![]() 在
在![]() 上恒成立,即函數
上恒成立,即函數![]() 在
在![]() 上單調遞增.
上單調遞增.
綜上所述,當![]() 時,函數
時,函數![]() 在
在![]() 上單調遞增;
上單調遞增;
當![]() 時,函數
時,函數![]() 在
在![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減;
上單調遞減;
(2)![]() ,當
,當![]() 時,由(1)結合函數
時,由(1)結合函數![]() 的單調性知,
的單調性知,
![]() ,使得對任意
,使得對任意![]() ,都有
,都有![]() ,則由
,則由![]() 得
得![]() .
.
設![]() ,則
,則![]() ,
,
由![]() 得
得![]() ,由
,由![]() 得
得![]() .
.
(Ⅰ)若![]() ,則
,則![]() ,故
,故![]() ,即函數
,即函數![]() 在
在![]() 上單調遞減,
上單調遞減,
![]() ,
,![]() 對任意
對任意![]() ,都有
,都有![]() ,不合題意;
,不合題意;
(Ⅱ)若![]() ,則
,則![]() ,故
,故![]() ,
,
![]() 在
在![]() 上單調遞增,
上單調遞增,
![]() ,
,![]() 對任意
對任意![]() ,都有
,都有![]() ,符合題意,
,符合題意,
此時取![]() ,可使得對
,可使得對![]() ,都有
,都有![]() .
.
綜上可得![]() 的取值范圍是
的取值范圍是![]() .
.


科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐中,底面![]() 為直角梯形,
為直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 為線段
為線段![]() 的中點.
的中點.
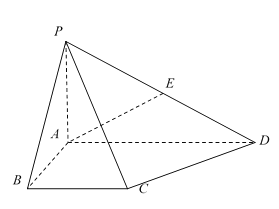
(Ⅰ)求直線![]() 與平面
與平面![]() 所成角的余弦值;
所成角的余弦值;
(Ⅱ)求二面角![]() 的大小;
的大小;
(Ⅲ)若![]() 在段
在段![]() 上,且直線
上,且直線![]() 與平面
與平面![]() 相交,求
相交,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設實數列![]() 滿足
滿足![]() ,則下面說法正確的是( )
,則下面說法正確的是( )
A.若![]() ,則
,則![]() 前2019項中至少有1010個值相等
前2019項中至少有1010個值相等
B.若![]() ,則當
,則當![]() 確定時,一定存在實數
確定時,一定存在實數![]() 使
使![]() 恒成立
恒成立
C.若![]() ,
,![]() 一定為等比數列
一定為等比數列
D.若![]() ,則當
,則當![]() 確定時,一定存在實數
確定時,一定存在實數![]() 使
使![]() 恒成立
恒成立
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】根據全球摩天大樓的統計,至2019年,安徽省合肥市的摩天大樓已經有95座在中國城市中排名第10位,全球排名第15位,目前合肥恒大中心建設中的最高樓,外形設計成了“竹節”的形態,既體現了力量超凡,又象征著向上生長的強烈意志,更預示了未來的繁榮和興旺.它與傳承千年的“微文化”相得益建成后將躋身世界十大摩天大樓之列,若大樓由9節“竹節”組成,最上部分的4節高228米,最下部分3節高204米,且每一節高度變化均勻(即每節高度自上而下成等差數列),則該摩天大樓的總高度為( )
A.518米B.558米C.588米D.668米
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com