
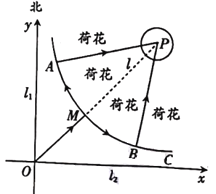
【題目】如圖,某市建有貫穿東西和南北的兩條垂直公路![]() ,
,![]() ,在它們交叉路口點(diǎn)
,在它們交叉路口點(diǎn)![]() 處的東北方向建有一個荷花池,荷花池的外圍是一條環(huán)形公路,荷花池中的固定觀景臺
處的東北方向建有一個荷花池,荷花池的外圍是一條環(huán)形公路,荷花池中的固定觀景臺![]() 位于兩條垂直公路的角平分線
位于兩條垂直公路的角平分線![]() 上,
上,![]() 與環(huán)形公路的交點(diǎn)記作
與環(huán)形公路的交點(diǎn)記作![]() .游客游覽荷花池時,需沿公路
.游客游覽荷花池時,需沿公路![]() 先到達(dá)環(huán)形公路
先到達(dá)環(huán)形公路![]() 處.為了分流游客,方便游客游覽荷花池,計(jì)劃從靠近公路
處.為了分流游客,方便游客游覽荷花池,計(jì)劃從靠近公路![]() ,
,![]() 的環(huán)形公路上選
的環(huán)形公路上選![]() ,
,![]() 兩處(
兩處(![]() ,
,![]() 關(guān)于直線
關(guān)于直線![]() 對稱)修建直達(dá)觀景臺
對稱)修建直達(dá)觀景臺![]() 的玻璃棧道
的玻璃棧道![]() ,
,![]() .以
.以![]() ,
,![]() 所在的直線為
所在的直線為![]() ,
,![]() 軸建立平面直角坐標(biāo)系
軸建立平面直角坐標(biāo)系![]() ,靠近公路
,靠近公路![]() ,
,![]() 的環(huán)形公路可用曲線
的環(huán)形公路可用曲線![]() 近似表示,曲線
近似表示,曲線![]() 符合函數(shù)
符合函數(shù)![]() .
.
(1)若![]() 百米,點(diǎn)
百米,點(diǎn)![]() 到
到![]() 的垂直距離為1百米,求玻璃棧道
的垂直距離為1百米,求玻璃棧道![]() 的總長度;
的總長度;
(2)若要使得玻璃棧道![]() 的總長度最小為
的總長度最小為![]() 百米,求觀景臺
百米,求觀景臺![]() 的位置.
的位置.
【答案】(1)![]() 百米.(2)
百米.(2)![]()
【解析】
(1)由![]() 百米可得
百米可得![]() ,點(diǎn)
,點(diǎn)![]() 到
到![]() 的垂直距離為1百米可得
的垂直距離為1百米可得![]() ,用平面兩點(diǎn)間的距離公式可求解答案.
,用平面兩點(diǎn)間的距離公式可求解答案.
(2)根據(jù)題意即![]() 的最小值為
的最小值為![]() ,設(shè)
,設(shè)![]() ,
,![]() ,則
,則![]() ,然后換元求出最值,解出
,然后換元求出最值,解出![]() 的值.
的值.
解:(1)在平面直角坐標(biāo)系![]() 中,設(shè)定點(diǎn)
中,設(shè)定點(diǎn)![]() ,
,
因?yàn)?/span>![]() ,所以
,所以![]() ,解得
,解得![]() ,即點(diǎn)
,即點(diǎn)![]() .
.
因?yàn)辄c(diǎn)![]() 到
到![]() 的垂直距離為1百米,所以點(diǎn)
的垂直距離為1百米,所以點(diǎn)![]() ;
;
所以![]() ,
,
又因?yàn)?/span>![]() ,
,![]() 關(guān)于直線
關(guān)于直線![]() 對稱,點(diǎn)
對稱,點(diǎn)![]() 在直線
在直線![]() 上,
上,
所以![]() .即
.即![]() .
.
所以玻璃棧道![]() 的總長度是
的總長度是![]() 百米.
百米.
(2)在平面直角坐標(biāo)系![]() 中,
中,![]() ,設(shè)定點(diǎn)
,設(shè)定點(diǎn)![]() ,
,
動點(diǎn)![]() ,因?yàn)?/span>
,因?yàn)?/span>![]() ,
,![]() 關(guān)于直線
關(guān)于直線![]() 對稱,
對稱,
點(diǎn)![]() 在直線
在直線![]() 上,所以
上,所以![]() .
.
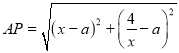 ,則
,則![]() ,
,
令![]() ,則
,則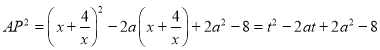 ,
,
函數(shù)![]() 的導(dǎo)數(shù)
的導(dǎo)數(shù)![]() ,
,
當(dāng)![]() 時,
時,![]() ,
,
所以![]() 在
在![]() 上單調(diào)減,所以
上單調(diào)減,所以![]()
函數(shù)![]() ,
,![]() 圖象對稱軸是
圖象對稱軸是![]() ,
,
當(dāng)![]() 時,
時,![]() 在區(qū)間
在區(qū)間![]() 上單調(diào)遞增,無最小值;
上單調(diào)遞增,無最小值;
當(dāng)![]() 時,
時,![]() 在
在![]() 上單調(diào)遞減,在
上單調(diào)遞減,在![]() 上單調(diào)遞增,
上單調(diào)遞增,
即![]() 在
在![]() 時有最小值
時有最小值![]() ,
,
由題意![]() ,因?yàn)?/span>
,因?yàn)?/span>![]() ,所以
,所以![]() .
.
所以若要使得玻璃棧道![]() 總長度最小為
總長度最小為![]() 百米,觀景平臺
百米,觀景平臺![]() 的坐標(biāo)是
的坐標(biāo)是![]() .
.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某同學(xué)用“隨機(jī)模擬方法”計(jì)算曲線![]() 與直線
與直線![]() 所圍成的曲邊三角形的面積時,用計(jì)算機(jī)分別產(chǎn)生了10個在區(qū)間[1,e]上的均勻隨機(jī)數(shù)xi和10個在區(qū)間[0,1]上的均勻隨機(jī)數(shù)
所圍成的曲邊三角形的面積時,用計(jì)算機(jī)分別產(chǎn)生了10個在區(qū)間[1,e]上的均勻隨機(jī)數(shù)xi和10個在區(qū)間[0,1]上的均勻隨機(jī)數(shù)![]()
![]() ,其數(shù)據(jù)如下表的前兩行.
,其數(shù)據(jù)如下表的前兩行.
x | 2.50 | 1.01 | 1.90 | 1.22 | 2.52 | 2.17 | 1.89 | 1.96 | 1.36 | 2.22 |
y | 0.84 | 0.25 | 0.98 | 0.15 | 0.01 | 0.60 | 0.59 | 0.88 | 0.84 | 0.10 |
lnx | 0.90 | 0.01 | 0.64 | 0.20 | 0.92 | 0.77 | 0.64 | 0.67 | 0.31 | 0.80 |
由此可得這個曲邊三角形面積的一個近似值為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】2020年,新冠狀肺炎疫情牽動每一個中國人的心,危難時刻眾志成城,共克時艱,為疫區(qū)助力.福建省漳州市東山縣共101個海鮮商家及個人為緩解武漢物質(zhì)壓力,募捐價值百萬的海鮮輸送武漢.東山島,別稱陵島,形似蝴蝶亦稱蝶島,隸屬于福建省漳州市東山縣,是福建省第二大島,中國第七大島,介于廈門市和廣東省汕頭之間,東南是著名的閩南漁場和粵東漁場交匯處,因地理位置發(fā)展海產(chǎn)品養(yǎng)殖業(yè)具有得天獨(dú)厚的優(yōu)勢.根據(jù)養(yǎng)殖規(guī)模與以往的養(yǎng)殖經(jīng)驗(yàn),某海鮮商家的海產(chǎn)品每只質(zhì)量(克)在正常環(huán)境下服從正態(tài)分布![]() .
.
(1)隨機(jī)購買10只該商家的海產(chǎn)品,求至少買到一只質(zhì)量小于265克該海產(chǎn)品的概率;
(2)2020年該商家考慮增加先進(jìn)養(yǎng)殖技術(shù)投入,該商家欲預(yù)測先進(jìn)養(yǎng)殖技術(shù)投入為49千元時的年收益增量.現(xiàn)用以往的先進(jìn)養(yǎng)殖技術(shù)投入![]() (千元)與年收益增量
(千元)與年收益增量![]() (千元).
(千元).![]() 的數(shù)據(jù)繪制散點(diǎn)圖,由散點(diǎn)圖的樣本點(diǎn)分布,可以認(rèn)為樣本點(diǎn)集中在曲線
的數(shù)據(jù)繪制散點(diǎn)圖,由散點(diǎn)圖的樣本點(diǎn)分布,可以認(rèn)為樣本點(diǎn)集中在曲線![]() 的附近,且
的附近,且![]()
![]()
![]()
![]()
![]() ,
,![]()
![]() ,其中
,其中![]()
![]() .根據(jù)所給的統(tǒng)計(jì)量,求y關(guān)于x的回歸方程,并預(yù)測先進(jìn)養(yǎng)殖技術(shù)投入為49千元時的年收益增量.
.根據(jù)所給的統(tǒng)計(jì)量,求y關(guān)于x的回歸方程,并預(yù)測先進(jìn)養(yǎng)殖技術(shù)投入為49千元時的年收益增量.
附:若隨機(jī)變量![]() ,則
,則![]()
![]() ;
;
對于一組數(shù)據(jù)![]()
![]()
![]()
![]() ,其回歸線
,其回歸線![]() 的斜率和截距的最小二乘估計(jì)分別為
的斜率和截距的最小二乘估計(jì)分別為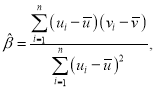
![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某地區(qū)人民法院每年要審理大量案件,去年審理的四類案件情況如表所示:
編號 | 項(xiàng)目 | 收案(件) | 結(jié)案(件) | |
判決(件) | ||||
1 | 刑事案件 | 2400 | 2400 | 2400 |
2 | 婚姻家庭、繼承糾紛案件 | 3000 | 2900 | 1200 |
3 | 權(quán)屬、侵權(quán)糾紛案件 | 4100 | 4000 | 2000 |
4 | 合同糾紛案件 | 14000 | 13000 | n |
其中結(jié)案包括:法庭調(diào)解案件、撤訴案件、判決案件等.根據(jù)以上數(shù)據(jù),回答下列問題.
(Ⅰ)在編號為1、2、3的收案案件中隨機(jī)取1件,求該件是結(jié)案案件的概率;
(Ⅱ)在編號為2的結(jié)案案件中隨機(jī)取1件,求該件是判決案件的概率;
(Ⅲ)在編號為1、2、3的三類案件中,判決案件數(shù)的平均數(shù)為![]() ,方差為S12,如果表中n
,方差為S12,如果表中n![]() ,表中全部(4類)案件的判決案件數(shù)的方差為S22,試判斷S12與S22的大小關(guān)系,并寫出你的結(jié)論(結(jié)論不要求證明).
,表中全部(4類)案件的判決案件數(shù)的方差為S22,試判斷S12與S22的大小關(guān)系,并寫出你的結(jié)論(結(jié)論不要求證明).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,正三角形ABE與菱形ABCD所在的平面互相垂直,![]() ,
,![]() ,M是AB的中點(diǎn),N是CE的中點(diǎn).
,M是AB的中點(diǎn),N是CE的中點(diǎn).
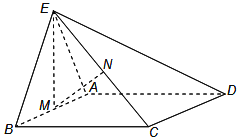
(1)求證:![]() ;
;
(2)求證:![]() 平面ADE;
平面ADE;
(3)求點(diǎn)A到平面BCE的距離.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】一批用于手電筒的電池,每節(jié)電池的壽命服從正態(tài)分布![]() (壽命單位:小時).考慮到生產(chǎn)成本,電池使用壽命在
(壽命單位:小時).考慮到生產(chǎn)成本,電池使用壽命在![]() 內(nèi)是合格產(chǎn)品.
內(nèi)是合格產(chǎn)品.
(1)求一節(jié)電池是合格產(chǎn)品的概率(結(jié)果四舍五入,保留一位小數(shù));
(2)根據(jù)(1)中的數(shù)據(jù)結(jié)果,若質(zhì)檢部門檢查4節(jié)電池,記抽查電池合格的數(shù)量為![]() ,求隨機(jī)變量
,求隨機(jī)變量![]() 的分布列、數(shù)學(xué)期望及方差.
的分布列、數(shù)學(xué)期望及方差.
附:若隨機(jī)變量![]() 服從正態(tài)分布
服從正態(tài)分布![]() ,則
,則![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知平行四邊形![]() 和矩形
和矩形![]() 所在平面垂直,其中
所在平面垂直,其中![]() 為棱
為棱![]() 的中點(diǎn),
的中點(diǎn),![]() 為
為![]() 的中點(diǎn).
的中點(diǎn).

(1)求證:![]() ;
;
(2)若點(diǎn)![]() 到平面
到平面![]() 的距離是
的距離是![]() ,求多面體
,求多面體![]() 的體積.
的體積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]()
(1)求函數(shù)![]() 的極值點(diǎn);
的極值點(diǎn);
(2)當(dāng)![]() 時,當(dāng)函數(shù)
時,當(dāng)函數(shù)![]() 恰有三個不同的零點(diǎn),求實(shí)數(shù)
恰有三個不同的零點(diǎn),求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com