
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 是直角梯形,側棱
是直角梯形,側棱![]() 底面
底面![]() ,
, ![]() 垂直于
垂直于![]() 和
和![]() ,
,![]() 為棱
為棱![]() 上的點,
上的點,![]() ,
,![]() .
.

(1)若![]() 為棱
為棱![]() 的中點,求證:
的中點,求證:![]() //平面
//平面![]() ;
;
(2)當![]() 時,求平面
時,求平面![]() 與平面
與平面![]() 所成的銳二面角的余弦值;
所成的銳二面角的余弦值;
(3)在第(2)問條件下,設點![]() 是線段
是線段![]() 上的動點,
上的動點,![]() 與平面
與平面![]() 所成的角為
所成的角為![]() ,求當
,求當![]() 取最大值時點
取最大值時點![]() 的位置.
的位置.
【答案】(1)見解析;(2)![]() ;(3)即點N在線段CD上且
;(3)即點N在線段CD上且![]()
【解析】
(1)取線段SC的中點E,連接ME,ED.可證![]() 是平行四邊形,從而有
是平行四邊形,從而有![]() ,則可得線面平行;
,則可得線面平行;
(2)以點A為坐標原點,建立分別以AD、AB、AS所在的直線為x軸、y軸、z軸建立空間直角坐標系,求出兩平面![]() 與平面
與平面![]() 的法向量,由法向量夾角的余弦值可得二面角的余弦值;
的法向量,由法向量夾角的余弦值可得二面角的余弦值;
(3)設![]() ,其中
,其中![]() ,求出
,求出![]() ,由MN與平面
,由MN與平面![]() 所成角的正弦值為
所成角的正弦值為![]() 與平面
與平面![]() 的法向量夾角余弦值的絕對值可求得結論.
的法向量夾角余弦值的絕對值可求得結論.
(1)證明:取線段SC的中點E,連接ME,ED.

在![]() 中,ME為中位線,∴
中,ME為中位線,∴![]() 且
且![]() ,
,
∵![]() 且
且![]() ,∴
,∴![]() 且
且![]() ,
,
∴四邊形AMED為平行四邊形.
∴![]() .
.
∵![]() 平面SCD,
平面SCD,![]() 平面SCD,
平面SCD,
∴![]() 平面SCD.
平面SCD.
(2)解:如圖所示以點A為坐標原點,建立分別以AD、AB、AS所在的直線為x軸、y軸、z軸建立空間直角坐標系,則![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
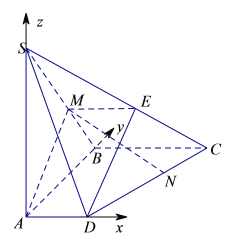
由條件得M為線段SB近B點的三等分點.
于是![]() ,即
,即![]() ,
,
設平面AMC的一個法向量為![]() ,則
,則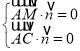 ,
,
將坐標代入并取![]() ,得
,得![]() .
.
另外易知平面SAB的一個法向量為![]()
![]() ,
,
所以平面AMC與平面SAB所成的銳二面角的余弦為![]()
![]() .
.
(3)設![]() ,其中
,其中![]() .
.
由于![]() ,所以
,所以![]()
![]() .
.
所以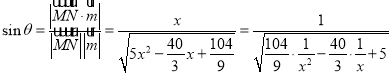 ,
,
可知當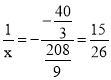 ,即
,即![]() 時分母有最小值,此時
時分母有最小值,此時![]() 有最大值,
有最大值,
此時,![]() ,即點N在線段CD上且
,即點N在線段CD上且![]() .
.


 陽光課堂課時作業系列答案
陽光課堂課時作業系列答案科目:高中數學 來源: 題型:
【題目】如圖所示,三棱柱![]() 的側棱垂直于底面,且底面是邊長為2的正三角形,
的側棱垂直于底面,且底面是邊長為2的正三角形,![]() ,點D,E,F分別是所在棱的中點.
,點D,E,F分別是所在棱的中點.

(1)在線段![]() 上找一點
上找一點![]() 使得平面
使得平面![]() ∥平面
∥平面![]() ,給出
,給出![]() 點的位置并證明你的結論;
點的位置并證明你的結論;
(2)在(1)的條件下,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】三國時期著名的數學家劉徽對推導特殊數列的求和公式很感興趣,創造并發展了許多算法,展現了聰明才智.他在《九章算術》“盈不足”章的第19題的注文中給出了一個特殊數列的求和公式.這個題的大意是:一匹良馬和一匹駑馬由長安出發至齊地,長安與齊地相距3000里(1里=500米),良馬第一天走193里,以后每天比前一天多走13里.駑馬第一天走97里,以后每天比前一天少走半里.良馬先到齊地后,馬上返回長安迎駑馬,問兩匹馬在第幾天相遇( )
A. 14天B. 15天C. 16天D. 17天
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】定義![]() 為
為![]() 個正數
個正數![]() 、
、![]() 、
、![]() 、
、![]() 的“均倒數”.已知正項數列
的“均倒數”.已知正項數列![]() 的前
的前![]() 項的“均倒數”為
項的“均倒數”為![]() .
.
(1)求數列![]() 的通項公式;
的通項公式;
(2)設數列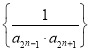 的前
的前![]() 項和為
項和為![]() ,若
,若![]() 對一切
對一切![]() 恒成立,試求實數
恒成立,試求實數![]() 的取值范圍;
的取值范圍;
(3)令![]() ,問:是否存在正整數
,問:是否存在正整數![]() 使得
使得![]() 對一切
對一切![]() 恒成立,如存在,求出
恒成立,如存在,求出![]() 值,否則說明理由.
值,否則說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】大氣污染是我國目前最突出的環境問題之一,其中工廠廢氣是大氣污染的重大污染源之一。工廠廢氣未經凈化處理排放至空氣中,除了對空氣質量造成嚴重破壞,還會對人體的健康造成重大威脅。長期生活在污染的空氣中,生活質量及身體健康將急劇下降。某工廠因為污染問題需改進技術,2019年初購進一臺環保新機器投入生產,機器的成本價為36萬元,第![]() 年該機器包括維修費和機器護理費用在內,每年另需投人費用
年該機器包括維修費和機器護理費用在內,每年另需投人費用![]() 萬元,購進該機器后每年盈利20萬元.
萬元,購進該機器后每年盈利20萬元.
(1)問該機器投入生產第幾年,工廠開始盈利(即總收入大于所有投人的費用)?
(2)由于機器使用年限越大維修等費用越高,所以工廠決定當年平均利潤最大時將該機器以5萬元低價處理,問使用該機器幾年后工廠年平均利潤最大?此時工廠獲得的總利潤為多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著經濟模式的改變,微商和電商已成為當今城鄉一種新型的購銷平臺.已知經銷某種商品的電商在任何一個銷售季度內,每售出![]() 噸該商品可獲利潤
噸該商品可獲利潤![]() 萬元,未售出的商品,每
萬元,未售出的商品,每![]() 噸虧損
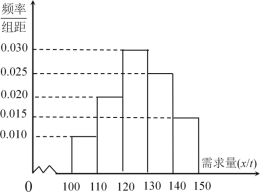
噸虧損![]() 萬元.根據往年的銷售經驗,得到一個銷售季度內市場需求量的頻率分布直方圖如圖所示.已知電商為下一個銷售季度籌備了
萬元.根據往年的銷售經驗,得到一個銷售季度內市場需求量的頻率分布直方圖如圖所示.已知電商為下一個銷售季度籌備了![]() 噸該商品.現以
噸該商品.現以![]() (單位:噸,
(單位:噸,![]() )表示下一個銷售季度的市場需求量,
)表示下一個銷售季度的市場需求量,![]() (單位:萬元)表示該電商下一個銷售季度內經銷該商品獲得的利潤.
(單位:萬元)表示該電商下一個銷售季度內經銷該商品獲得的利潤.
(1)將![]() 表示為
表示為![]() 的函數,求出該函數表達式;
的函數,求出該函數表達式;
(2)根據直方圖估計利潤![]() 不少于57萬元的概率;
不少于57萬元的概率;
(3)根據頻率分布直方圖,估計一個銷售季度內市場需求量![]() 的平均數與中位數的大小(保留到小數點后一位).
的平均數與中位數的大小(保留到小數點后一位).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點![]() 是圓
是圓![]() :
:![]() 上的一動點,點
上的一動點,點![]() ,點
,點![]() 在線段
在線段![]() 上,且滿足
上,且滿足![]() .
.
(1)求點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(2)設曲線![]() 與
與![]() 軸的正半軸,
軸的正半軸,![]() 軸的正半軸的交點分別為點
軸的正半軸的交點分別為點![]() ,
,![]() ,斜率為
,斜率為![]() 的動直線
的動直線![]() 交曲線
交曲線![]() 于
于![]() 、
、![]() 兩點,其中點
兩點,其中點![]() 在第一象限,求四邊形
在第一象限,求四邊形![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com