
【題目】如圖,在三棱柱![]() 中,
中,![]() 是邊長為4的正方形,平面
是邊長為4的正方形,平面![]() 平面
平面![]() ,
,![]() ,
,![]() .
.

(1)求二面角![]() 的余弦值;
的余弦值;
(2)在線段![]() 是否存在點
是否存在點![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
【答案】(1)![]() .(2)存在,值為
.(2)存在,值為![]()
【解析】
(1)建立空間直角坐標(biāo)系,利用平面![]() 的法向量和平面
的法向量和平面![]() 的法向量,計算出二面角
的法向量,計算出二面角![]() 的余弦值.
的余弦值.
(2)首先利用![]() 求得
求得![]() 點的坐標(biāo),由
點的坐標(biāo),由![]() 求得
求得![]() 的值.
的值.
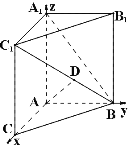
(1)因為![]() 為正方形,所以
為正方形,所以![]() .
.
因為平面ABC⊥平面![]() ,且
,且![]() 垂直于這兩個平面的交線
垂直于這兩個平面的交線![]() ,所以
,所以![]() 平面
平面![]() .由題知
.由題知![]() ,
,![]() ,
,![]() ,所以
,所以![]() .如圖,以
.如圖,以![]() 為原點建立空間直角坐標(biāo)系
為原點建立空間直角坐標(biāo)系![]() ,則
,則![]() ,
,![]() ,
,![]() ,
,![]() ,設(shè)平面
,設(shè)平面![]() 的法向量為
的法向量為![]() ,則
,則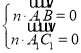 ,即
,即![]() ,
,
令![]() ,則
,則![]() ,
,![]() ,所以
,所以![]() .
.
同理可得,平面![]() 的法向量為
的法向量為![]() ,所以
,所以![]() .由題知二面角
.由題知二面角![]() 為銳角,所以二面角
為銳角,所以二面角![]() 的余弦值為
的余弦值為![]() .
.
(2)存在.設(shè)![]() 是直線
是直線![]() 上一點,且
上一點,且![]() .所以
.所以![]() .解得
.解得![]() ,
,![]() ,
,![]() .
.
所以![]() .
.
由![]() ,即
,即![]() .解得
.解得![]() .
.
因為![]() ,所以在線段
,所以在線段![]() 上存在點
上存在點![]() ,
,
使得![]() .此時,
.此時,![]() .
.


 七星圖書口算速算天天練系列答案
七星圖書口算速算天天練系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】(本小題滿分14分)已知過原點的動直線![]() 與圓
與圓![]()
![]() 相交于不同的兩點
相交于不同的兩點![]() ,
,![]() .
.
(1)求圓![]() 的圓心坐標(biāo);
的圓心坐標(biāo);
(2)求線段![]() 的中點
的中點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(3)是否存在實數(shù)![]() ,使得直線
,使得直線![]()
![]() 與曲線
與曲線![]() 只有一個交點?若存在,求出
只有一個交點?若存在,求出![]() 的取值范圍;若不存在,說明理由.
的取值范圍;若不存在,說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在△ABC中,a,b,c分別為內(nèi)角A,B,C的對邊,且asin B=-bsin![]() .
.
(1)求A;
(2)若△ABC的面積S=![]() c2,求sin C的值.
c2,求sin C的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() ,
,![]() .
.
(1)求函數(shù)![]() 的最小正周期;
的最小正周期;
(2)求函數(shù)![]() 的單調(diào)遞增區(qū)間;
的單調(diào)遞增區(qū)間;
(3)若把![]() 向右平移
向右平移![]() 個單位得到函數(shù)
個單位得到函數(shù)![]() ,求
,求![]() 在區(qū)間
在區(qū)間![]() 上的最小值和最大值.
上的最小值和最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在四棱錐P-ABCD中,PA⊥平面ABCD,AB⊥AD,AD∥BC,AP=AB=AD=1.
(Ⅰ)若直線PB與CD所成角的大小為![]() ,求BC的長;
,求BC的長;
(Ⅱ)求二面角B-PD-A的余弦值.

查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】從![]() 、
、![]() 、
、![]() 、
、![]() 這
這![]() 個數(shù)中一次隨機地取
個數(shù)中一次隨機地取![]() 個數(shù),記所取的這
個數(shù),記所取的這![]() 個數(shù)的和為
個數(shù)的和為![]() ,則下列說法錯誤的是( )
,則下列說法錯誤的是( )
A.事件“![]() ”的概率為
”的概率為![]()
B.事件“![]() ”的概率為
”的概率為![]()
C.事件“![]() ”與事件“
”與事件“![]() ”為互斥事件
”為互斥事件
D.事件“![]() ”與事件“
”與事件“![]() ”互為對立事件
”互為對立事件
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】稱直角坐標(biāo)系中縱橫坐標(biāo)均為整數(shù)的 點為“格點”,稱一格點沿坐標(biāo)線到原點的最短路程為該點到原點的“格點距離”,格點距離為定值的點的軌跡稱為“格點圓”,該定值稱為格點圓的半徑,而每一條最短路程稱為一條半徑.當(dāng)格點半徑為2005時,格點圓的半徑有________條.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某網(wǎng)紅直播平臺為確定下一季度的廣告投入計劃,收集了近6個月廣告投入量![]() (單位:萬元)和收益
(單位:萬元)和收益![]() (單位:萬元)的數(shù)據(jù)如下表:
(單位:萬元)的數(shù)據(jù)如下表:
月份 | 1 | 2 | 3 | 4 | 5 | 6 |
廣告投入量/萬元 | 2 | 4 | 6 | 8 | 10 | 12 |
收益/萬元 | 14.21 | 20.31 | 31.8 | 31.18 | 37.83 | 44.67 |
用兩種模型①![]() ,②
,②![]() 分別進(jìn)行擬合,得到相應(yīng)的回歸方程并進(jìn)行殘差分析,得到如圖所示的殘差圖及一些統(tǒng)計量的值:
分別進(jìn)行擬合,得到相應(yīng)的回歸方程并進(jìn)行殘差分析,得到如圖所示的殘差圖及一些統(tǒng)計量的值:
|
|
|
|
7 | 30 | 1464.24 | 364 |
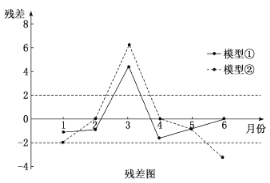
(1)根據(jù)殘差圖,比較模型①,②的擬合效果,應(yīng)選擇哪個模型?并說明理由.
(2)殘差絕對值大于2的數(shù)據(jù)被認(rèn)為是異常數(shù)據(jù),需要剔除:
(i)剔除的異常數(shù)據(jù)是哪一組?
(ii)剔除異常數(shù)據(jù)后,求出(1)中所選模型的回歸方程;
(iii)廣告投入量![]() 時,(ii)中所得模型收益的預(yù)報值是多少?
時,(ii)中所得模型收益的預(yù)報值是多少?
附:對于一組數(shù)據(jù)![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計分別為:
的斜率和截距的最小二乘估計分別為: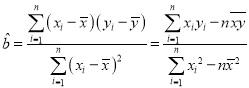 ,
,![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】建造一條防洪堤,其斷面為等腰梯形,腰與底邊成角為![]() ,防洪堤高記為
,防洪堤高記為![]() (如圖),考慮到防洪堤堅固性及石塊用料等因素,設(shè)計其斷面面積為
(如圖),考慮到防洪堤堅固性及石塊用料等因素,設(shè)計其斷面面積為![]() 平方米,為了使堤的上面與兩側(cè)面的水泥用料最省,則斷面的外周長
平方米,為了使堤的上面與兩側(cè)面的水泥用料最省,則斷面的外周長![]() (
(![]() )要最小.
)要最小.

(1)用![]() 表示
表示![]() 、
、![]() ;
;
(2)將![]() 表示成
表示成![]() 的函數(shù)
的函數(shù)![]() ,如
,如![]() 限制在
限制在![]() 范圍內(nèi),
范圍內(nèi),![]() 最小為多少米?并說明理由.
最小為多少米?并說明理由.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com