
【題目】橢圓![]() 的離心率是
的離心率是![]() ,過點
,過點![]() 做斜率為
做斜率為![]() 的直線
的直線![]() ,橢圓
,橢圓![]() 與直線
與直線![]() 交于
交于![]() 兩點,當直線
兩點,當直線![]() 垂直于
垂直于![]() 軸時
軸時![]() .
.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)當![]() 變化時,在
變化時,在![]() 軸上是否存在點
軸上是否存在點![]() ,使得
,使得![]() 是以
是以![]() 為底的等腰三角形,若存在求出
為底的等腰三角形,若存在求出![]() 的取值范圍,若不存在說明理由.
的取值范圍,若不存在說明理由.
【答案】(Ⅰ) ![]() ;(Ⅱ)見解析。
;(Ⅱ)見解析。
【解析】
(Ⅰ)由橢圓的離心率為![]() 得到
得到![]() ,于是橢圓方程為
,于是橢圓方程為![]() .有根據題意得到橢圓過點
.有根據題意得到橢圓過點![]() ,將坐標代入方程后求得
,將坐標代入方程后求得![]() ,進而可得橢圓的方程.(Ⅱ)假設存在點
,進而可得橢圓的方程.(Ⅱ)假設存在點![]() ,使得
,使得![]() 是以
是以![]() 為底的等腰三角形,則點
為底的等腰三角形,則點![]() 為線段AB的垂直平分線與x軸的交點.由題意得設出直線
為線段AB的垂直平分線與x軸的交點.由題意得設出直線![]() 的方程,借助二次方程的知識求得線段
的方程,借助二次方程的知識求得線段![]() 的中點
的中點![]() 的坐標,進而得到線段
的坐標,進而得到線段![]() 的垂直平分線的方程,在求出點
的垂直平分線的方程,在求出點![]() 的坐標后根據基本不等式可求出
的坐標后根據基本不等式可求出![]() 的取值范圍.
的取值范圍.
(Ⅰ)因為橢圓的離心率為![]() ,
,
所以![]() ,整理得
,整理得![]() .
.
故橢圓的方程為![]() .
.
由已知得橢圓過點![]() ,
,
所以![]() ,解得
,解得![]() ,
,
所以橢圓的![]() 方程為
方程為![]() .
.
(Ⅱ)由題意得直線![]() 的方程為
的方程為![]() .
.
由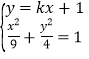 消去
消去![]() 整理得
整理得![]() ,
,
其中![]() .
.
設![]() ,
,![]() 的中點
的中點![]()
則![]() ,
,
所以![]()
∴![]() ,
,
∴點C的坐標為![]() .
.
假設在![]() 軸存在點
軸存在點![]() ,使得
,使得![]() 是以
是以![]() 為底的等腰三角形,
為底的等腰三角形,
則點![]() 為線段
為線段![]() 的垂直平分線與x軸的交點.
的垂直平分線與x軸的交點.
①當![]() 時,則過點
時,則過點![]() 且與
且與![]() 垂直的直線方程
垂直的直線方程![]() ,
,
令![]() ,則得
,則得![]() .
.
若![]() ,則
,則![]() ,
,
∴![]() .
.
若![]() ,則
,則![]() ,
,
∴![]() .
.
②當![]() 時,則有
時,則有![]() .
.
綜上可得![]() .
.
所以存在點![]() 滿足條件,且m的取值范圍是
滿足條件,且m的取值范圍是![]() .
.


 新思維假期作業暑假吉林大學出版社系列答案
新思維假期作業暑假吉林大學出版社系列答案 藍天教育暑假優化學習系列答案
藍天教育暑假優化學習系列答案科目:高中數學 來源: 題型:
【題目】某保險公司對一個擁有20000人的企業推出一款意外險產品,每年每位職工只要交少量保費,發生意外后可一次性獲得若干賠償金,保險公司把企業的所有崗位共分為![]() 三類工種,從事這三類工種的人數分別為12000,6000,2000,由歷史數據統計出三類工種的賠付頻率如下表(并以此估計賠付概率):
三類工種,從事這三類工種的人數分別為12000,6000,2000,由歷史數據統計出三類工種的賠付頻率如下表(并以此估計賠付概率):
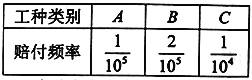
已知![]() 三類工種職工每人每年保費分別為25元、25元、40元,出險后的賠償金額分別為100萬元、100萬元、50萬元,保險公司在開展此項業務過程中的固定支出為每年10萬元.
三類工種職工每人每年保費分別為25元、25元、40元,出險后的賠償金額分別為100萬元、100萬元、50萬元,保險公司在開展此項業務過程中的固定支出為每年10萬元.
(1)求保險公司在該業務所或利潤的期望值;
(2)現有如下兩個方案供企業選擇:
方案1:企業不與保險公司合作,職工不交保險,出意外企業自行拿出與保險公司提供的等額賠償金賠償付給意外職工,企業開展這項工作的固定支出為每年12萬元;
方案2:企業與保險公司合作,企業負責職工保費的70%,職工個人負責保費的30%,出險后賠償金由保險公司賠付,企業無額外專項開支.
請根據企業成本差異給出選擇合適方案的建議.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】費馬點是指三角形內到三角形三個頂點距離之和最小的點。當三角形三個內角均小于![]() 時,費馬點與三個頂點連線正好三等分費馬點所在的周角,即該點所對的三角形三邊的張角相等均為
時,費馬點與三個頂點連線正好三等分費馬點所在的周角,即該點所對的三角形三邊的張角相等均為![]() 。根據以上性質,函數
。根據以上性質,函數![]() 的最小值為__________.
的最小值為__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() 滿足
滿足![]() ,且
,且![]() ,點
,點![]() 在二次函數
在二次函數![]() 的圖象上.
的圖象上.
(1)試判斷數列![]() 是否為算術平方根遞推數列?若是,請說明你的理由;
是否為算術平方根遞推數列?若是,請說明你的理由;
(2)記![]() ,求證:數列
,求證:數列![]() 是等比數列,并求出通項公式
是等比數列,并求出通項公式![]() ;
;
(3)在數列![]() 中依據某種順序從左至右取出其中的項
中依據某種順序從左至右取出其中的項![]() ,…,把這些項重新組成一個新數列
,…,把這些項重新組成一個新數列![]() ,….若數列
,….若數列![]() 是首項為
是首項為![]() 、公比為
、公比為![]() 的無窮等比數列,且數列
的無窮等比數列,且數列![]() 各項的和為
各項的和為![]() ,求正整數
,求正整數![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
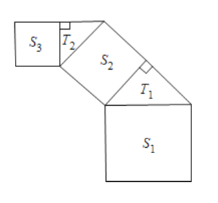
【題目】如圖所示,正方形上連接等腰直角三角形,直角三角形上再連接正方形……如此無限重復下去,設正方形面積為![]() ,三角形面積為
,三角形面積為![]() .當第一個正方形的邊長為2時,則這些正方形和三角形的面積的總和為______.
.當第一個正方形的邊長為2時,則這些正方形和三角形的面積的總和為______.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓E:![]() 的離心率為
的離心率為![]() ,且過點
,且過點![]()
![]() 求橢圓E的方程;
求橢圓E的方程;
![]() 設直線
設直線![]() 與橢圓E交于A、B兩點,與x軸、y軸分別交于C、D兩點
與橢圓E交于A、B兩點,與x軸、y軸分別交于C、D兩點![]() 且C、D在A、B之間或同時在A、B之外
且C、D在A、B之間或同時在A、B之外![]() 問:是否存在定值k,使得
問:是否存在定值k,使得![]() 的面積與
的面積與![]() 的面積總相等,若存在,求k的值,并求出實數m取值范圍;若不存在,說明理由.
的面積總相等,若存在,求k的值,并求出實數m取值范圍;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某賓館有50個房間供游客居住,當每個房間定價為每天180元時,房間會全部住滿;房間單價增加10元,就會有一個房間空閑,如果游客居住房間,賓館每間每天需花費20元的各種維護費用.房間定價多少時,賓館利潤最大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設四邊形![]() 為矩形,點
為矩形,點![]() 為平面
為平面![]() 外一點,且
外一點,且![]() 平面
平面![]() ,若
,若![]() ,
,![]() .
.
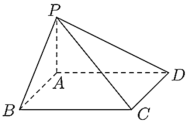
(1)求![]() 與平面
與平面![]() 所成角的大小;
所成角的大小;
(2)在![]() 邊上是否存在一點
邊上是否存在一點![]() ,使得點
,使得點![]() 到平面
到平面![]() 的距離為
的距離為![]() ,若存在,求出
,若存在,求出![]() 的值,若不存在,請說明理由;
的值,若不存在,請說明理由;
(3)若點![]() 是
是![]() 的中點,在
的中點,在![]() 內確定一點
內確定一點![]() ,使
,使![]() 的值最小,并求此時
的值最小,并求此時![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com