
【題目】某人某天的工作是駕車從![]() 地出發,到
地出發,到![]() 兩地辦事,最后返回
兩地辦事,最后返回![]() 地,
地,![]() ,三地之間各路段行駛時間及擁堵概率如下表
,三地之間各路段行駛時間及擁堵概率如下表
路段 | 正常行駛所用時間(小時) | 上午擁堵概率 | 下午擁堵概率 |
| 1 | 0.3 | 0.6 |
| 2 | 0.2 | 0.7 |
| 3 | 0.3 | 0.9 |
若在某路段遇到擁堵,則在該路段行駛時間需要延長1小時.
現有如下兩個方案:
方案甲:上午從![]() 地出發到
地出發到![]() 地辦事然后到達
地辦事然后到達![]() 地,下午從
地,下午從![]() 地辦事后返回
地辦事后返回![]() 地;
地;
方案乙:上午從![]() 地出發到
地出發到![]() 地辦事,下午從
地辦事,下午從![]() 地出發到達
地出發到達![]() 地,辦完事后返回
地,辦完事后返回![]() 地.
地.
(1)若此人早上8點從![]() 地出發,在各地辦事及午餐的累積時間為2小時,且采用方案甲,求他當日18點或18點之前能返回
地出發,在各地辦事及午餐的累積時間為2小時,且采用方案甲,求他當日18點或18點之前能返回![]() 地的概率.
地的概率.
(2)甲乙兩個方案中,哪個方案有利于辦完事后更早返回![]() 地?請說明理由.
地?請說明理由.
【答案】(1)![]() ;(2)采用甲方案能更早返回,理由見解析.
;(2)采用甲方案能更早返回,理由見解析.
【解析】
(1)由題意可知能按時返回的充要條件是擁堵路段不超過兩段,則不能按時,返回時由三段擁堵,二者互為對立事件,利用對立事件的概率公式,即可求解.
(2)設某段路正常行駛時間為![]() ,擁堵的概率為
,擁堵的概率為![]() ,可得該路段行駛時間
,可得該路段行駛時間![]() 的分布列,利用公式求得期望.
的分布列,利用公式求得期望.
(1)由題可知能按時返回的充要條件是擁堵路段不超過兩段,則不能按時返回時有三段路段擁堵,二者互為對立事件,記“不能按時返回為事件![]() ”則
”則![]() ,
,
所以能夠按時返回的概率![]() ,
,
(2)設某段路正常行駛時間為![]() ,擁堵的概率為
,擁堵的概率為![]() ,
,
則該路段行駛時間![]() 的分布列為
的分布列為
行駛時間 |
|
|
概率 |
|
|
故![]() ,
,
上午![]() 路段行駛時間期望值分別為1.3小時2.2小時、3.3小時,
路段行駛時間期望值分別為1.3小時2.2小時、3.3小時,
下午![]() 路段行駛時間期望值分別為1.6小時2.7小時3.9小時,
路段行駛時間期望值分別為1.6小時2.7小時3.9小時,
設采用甲方案所花費總行駛時間為![]() ,則
,則![]() 小時,
小時,
設采用乙方案所花費總行駛時間為Z,則EZ=3.3+2.7+1.6=7.6小時,
因此采用甲方案能更早返回.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】每年3月20日是國際幸福日,某電視臺隨機調查某一社區人們的幸福度.現從該社區群中隨機抽取18名,用“10分制”記錄了他們的幸福度指數,結果見如圖所示莖葉圖,其中以小數點前的一位數字為莖,小數點后的一位數字為葉.若幸福度不低于8.5分,則稱該人的幸福度為“很幸福”.
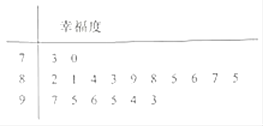
(Ⅰ)求從這18人中隨機選取3人,至少有1人是“很幸福”的概率;
(Ⅱ)以這18人的樣本數據來估計整個社區的總體數據,若從該社區(人數很多)任選3人,記![]() 表示抽到“很幸福”的人數,求
表示抽到“很幸福”的人數,求![]() 的分布列及
的分布列及![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某單位計劃在一水庫建一座至多安裝3臺發電機的水電站,過去50年的水文資料顯示,水庫年入流量![]() (年入流量:一年內上游來水與庫區降水之和,單位:億立方米)都在40以上,不足80的年份有10年,不低于80且不超過120的年份有35年,超過120的年份有5年,將年入流量在以上三段的頻率作為相應段的概率,假設各年的年入流量相互獨立.
(年入流量:一年內上游來水與庫區降水之和,單位:億立方米)都在40以上,不足80的年份有10年,不低于80且不超過120的年份有35年,超過120的年份有5年,將年入流量在以上三段的頻率作為相應段的概率,假設各年的年入流量相互獨立.
(1)求未來3年中,設![]() 表示流量超過120的年數,求
表示流量超過120的年數,求![]() 的分布列及期望;
的分布列及期望;
(2)水電站希望安裝的發電機盡可能運行,但每年發電機最多可運行臺數受年入流量![]() 限制,并有如下關系:
限制,并有如下關系:
年入流量 |
|
|
|
發電機最多可運行臺數 | 1 | 2 | 3 |
若某臺發電機運行,則該臺年利潤為5000萬元,若某臺發電機未運行,則該臺年虧損800萬元,欲使水電站年總利潤的均值達到最大,應安裝發電機多少臺?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】十九世紀末,法國學者貝特朗在研究幾何概型時提出了“貝特朗悖論”,即“在一個圓內任意選一條弦,這條弦的弦長長于這個圓的內接等邊三角形邊長的概率是多少?”貝特朗用“隨機半徑”、“隨機端點”、“隨機中點”三個合理的求解方法,但結果都不相同.該悖論的矛頭直擊概率概念本身,強烈地刺激了概率論基礎的嚴格化.已知“隨機端點”的方法如下:設A為圓O上一個定點,在圓周上隨機取一點B,連接AB,所得弦長AB大于圓O的內接等邊三角形邊長的概率.則由“隨機端點”求法所求得的概率為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】中國古代中的“禮、樂、射、御、書、數”合稱“六藝”.“禮”,主要指德育;“樂”,主要指美育;“射”和“御”,就是體育和勞動;“書”,指各種歷史文化知識;“數”,指數學.某校國學社團開展“六藝”課程講座活動,每藝安排一節,連排六節,一天課程講座排課有如下要求:“數”必須排在第三節,且“射”和“御”兩門課程相鄰排課,則“六藝”課程講座不同的排課順序共有( )
A.12種B.24種C.36種D.48種
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設數列![]() 的前n項和為
的前n項和為![]() ,已知
,已知![]() ,
,![]() ,
,![]() .
.
(1)證明:![]() 為等比數列,求出
為等比數列,求出![]() 的通項公式;
的通項公式;
(2)若![]() ,求
,求![]() 的前n項和
的前n項和![]() ,并判斷是否存在正整數n使得
,并判斷是否存在正整數n使得![]() 成立?若存在求出所有n值;若不存在說明理由.
成立?若存在求出所有n值;若不存在說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com