Question

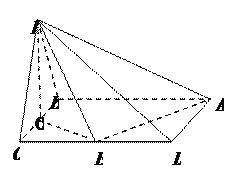
【題目】如圖，在四棱錐中，底面為矩形，平面平面，．　

（1）證明：平面平面；

（2）若，為棱的中點，，，求四面體的體積．

Answer 1

【答案】（1）見解析；（2）

【解析】分析：(1)由面面垂直的性質定理得到⊥平面，即，進而得到平面平面,(2)由等體積法求解，。

詳解：（1）證明：∵四邊形是矩形，∴CD⊥BC.

∵平面PBC⊥平面ABCD，平面PBC∩平面ABCD=BC，CD平面ABCD，

∴CD⊥平面PBC，∴CD⊥PB.

∵PB⊥PD，CD∩PD=D，CD、PD平面PCD，∴PB⊥平面PCD.

∵PB平面PAB，∴平面PAB⊥平面PCD.

（2）取BC的中點O，連接OP、OE.

∵平面，∴，∴，

∵，∴．

∵平面PBC⊥平面ABCD，平面PBC∩平面ABCD=BC，PO平面PBC，

∴PO⊥平面ABCD，∵AE平面ABCD,∴PO⊥AE.∵∠PEA=90O, ∴PE⊥AE.

∵PO∩PE=P，∴AE⊥平面POE，∴AE⊥OE.

∵∠C=∠D=90O, ∴∠OEC=∠EAD,

∴，∴．

∵，，，∴，

．