
【題目】中國古代中的“禮、樂、射、御、書、數”合稱“六藝”.“禮”,主要指德育;“樂”,主要指美育;“射”和“御”,就是體育和勞動;“書”,指各種歷史文化知識;“數”,指數學.某校國學社團開展“六藝”課程講座活動,每藝安排一節,連排六節,一天課程講座排課有如下要求:“數”必須排在第三節,且“射”和“御”兩門課程相鄰排課,則“六藝”課程講座不同的排課順序共有( )
A.12種B.24種C.36種D.48種
 輕松課堂單元期中期末專題沖刺100分系列答案
輕松課堂單元期中期末專題沖刺100分系列答案科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P﹣ABCD中,底面ABCD是菱形,且∠DAB=60°.點E是棱PC的中點,平面ABE與棱PD交于點F.
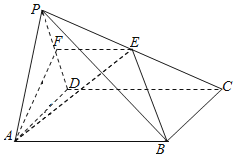
(1)求證:AB∥EF;
(2)若PA=PD=AD,且平面PAD⊥平面ABCD,求平面PAF與平面AFE所成的銳二面角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,圓
中,圓![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),以
為參數),以![]() 為極點,
為極點,![]() 軸的非負半軸為極軸建極坐標系,直線
軸的非負半軸為極軸建極坐標系,直線![]() 的極坐標方程為
的極坐標方程為![]()
(Ⅰ)求![]() 的極坐標方程;
的極坐標方程;
(Ⅱ)射線![]() 與圓C的交點為
與圓C的交點為![]() 與直線
與直線![]() 的交點為
的交點為![]() ,求
,求![]() 的范圍.
的范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 為偶函數,且函數
為偶函數,且函數![]() 圖象的兩相鄰對稱軸間的距離為
圖象的兩相鄰對稱軸間的距離為![]() .
.
(1)求![]() 的值;
的值;
(2)求函數![]() 的對稱軸方程;
的對稱軸方程;
(3)當![]() 時,方程
時,方程![]() 有兩個不同的實根,求m的取值范圍。
有兩個不同的實根,求m的取值范圍。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() 滿足
滿足![]() ,且
,且![]() .
.
(Ⅰ)求![]() ,
,![]() 的值;
的值;
(Ⅱ)是否存在實數![]() ,
,![]() ,使得
,使得 ,對任意正整數
,對任意正整數![]() 恒成立?若存在,求出實數
恒成立?若存在,求出實數![]() 、
、![]() 的值并證明你的結論;若不存在,請說明理由.
的值并證明你的結論;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】以下莖葉圖記錄了甲、乙兩組各四名同學的植樹棵數。乙組記錄中有一個數據模糊,無法確認,在圖中經X表示。
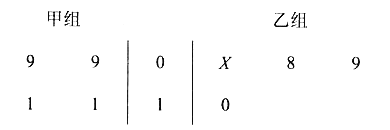
(1)如果X=8,求乙組同學植樹棵數的平均數和方差
(2)如果X=9,分別從甲、乙兩組中隨機選取一名同學,求這兩名同學的植樹總棵數為19的概率
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com