
【題目】已知三次函數![]() 在
在![]() 和
和![]() 處取得極值,且
處取得極值,且![]() 在
在![]() 處的切線方程為
處的切線方程為![]() .
.
(1)若函數![]() 的圖象上有兩條與
的圖象上有兩條與![]() 軸平行的切線,求實數
軸平行的切線,求實數![]() 的取值范圍;
的取值范圍;
(2)若函數![]() 與
與![]() 在
在![]() 上有兩個交點,求實數
上有兩個交點,求實數![]() 的取值范圍.
的取值范圍.
科目:高中數學 來源: 題型:
【題目】某公司生產了![]() 兩種產品投放市場,計劃每年對這兩種產品托人200萬元,每種產品一年至少投入20萬元,其中
兩種產品投放市場,計劃每年對這兩種產品托人200萬元,每種產品一年至少投入20萬元,其中![]() 產品的年收益
產品的年收益![]() ,
,![]() 產品的年收益
產品的年收益![]() 與投入
與投入![]() (單位萬元)分別滿足
(單位萬元)分別滿足![]() ;若公司有100名銷售人員,按照對兩種產品的銷售業績分為普銷售、中級銷售以及金牌銷售,其中普銷售28人,中級銷售60人,金牌銷售12人
;若公司有100名銷售人員,按照對兩種產品的銷售業績分為普銷售、中級銷售以及金牌銷售,其中普銷售28人,中級銷售60人,金牌銷售12人
(1)為了使![]() 兩種產品的總收益之和最大,求
兩種產品的總收益之和最大,求![]() 產品每年的投入
產品每年的投入
(2)為了對表現良好的銷售人員進行獎勵,公司制定了兩種獎勵方案:
方案一:按分層抽樣從三類銷售中總共抽取25人給予獎勵:普通銷售獎勵2300元,中級銷售獎勵5000元;金牌銷售獎勵8000元
方案二:每位銷售都參加摸獎游戲,游戲規則:從一個裝有3個白球,2個紅球(求只有顏色不同)的箱子中,有放回地莫三次球,每次只能摸一只球.若摸到紅球的總數為2,則可獎勵1500元,若摸到紅球總數是3,則可獲得獎勵3000元,其他情況不給予獎勵,規定普通銷售均可參加1次摸獎游戲;中級銷售均可參加2次摸獎游戲,金牌銷售均可參加3次摸獎游戲(每次摸獎的結果相互獨立,獎勵疊加)
(ⅰ)求方案一獎勵的總金額;
(ⅱ)假設你是企業老板,試通過計算并結合實際說明,你會選擇哪種方案獎勵銷售員.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(本小題滿分12分)如圖,三棱柱ABC-A1B1C1中,CA=CB,AB=A A1,∠BA A1=60°.
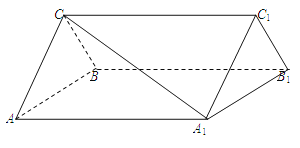
(Ⅰ)證明AB⊥A1C;
(Ⅱ)若平面ABC⊥平面AA1B1B,AB=CB,求直線A1C 與平面BB1C1C所成角的正弦值。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知中心在原點![]() ,焦點在
,焦點在![]() 軸上,離心率為
軸上,離心率為![]() 的橢圓過點
的橢圓過點![]()

(1)求橢圓的方程;
(2)設不過原點![]() 的直線
的直線![]() 與該橢圓交于
與該橢圓交于![]() 兩點,滿足直線
兩點,滿足直線![]() 的斜率依次成等比數列,求
的斜率依次成等比數列,求![]() 面積的取值范圍.
面積的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(多選)已知函數![]() ,其中正確結論的是( )
,其中正確結論的是( )
A.當![]() 時,函數
時,函數![]() 有最大值.
有最大值.
B.對于任意的![]() ,函數
,函數![]() 一定存在最小值.
一定存在最小值.
C.對于任意的![]() ,函數
,函數![]() 是
是![]() 上的增函數.
上的增函數.
D.對于任意的![]() ,都有函數
,都有函數![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com