
已知關于x的函數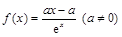
(1)當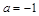 時,求函數
時,求函數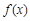 的極值;
的極值;
(2)若函數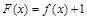 沒有零點,求實數a取值范圍.
沒有零點,求實數a取值范圍.
(1)函數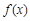 的極小值為
的極小值為 ;(2)
;(2)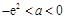 .
.
解析試題分析:(1)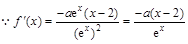 ,當
,當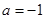 時,
時,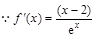
可利用導函數的符號判斷函數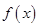 的單調性并求得極值;
的單調性并求得極值;
(2)要使函數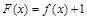 沒有零點,可借助導數研究函數
沒有零點,可借助導數研究函數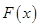 的單調性及極值,參數
的單調性及極值,參數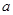 的值要確保
的值要確保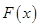 在定義域內恒正(或恒負),即函數
在定義域內恒正(或恒負),即函數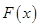 的最小值為正,或最大值為負,并由此求出
的最小值為正,或最大值為負,并由此求出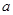 的取值范圍.
的取值范圍.
試題解析:
解:(1)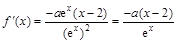 ,
,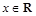 . 2分
. 2分
當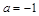 時,
時,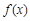 ,
,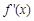 的情況如下表:
的情況如下表:
所以,當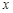
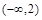
2 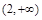
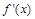
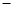
0 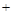
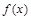
↘ 極小值 ↗ 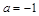 時,函數
時,函數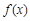 的極小值為
的極小值為 . 6分
. 6分
(2)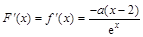 . 7分
. 7分
當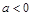 時,
時,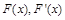 的情況如下表:
的情況如下表: