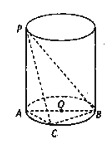
【題目】如圖所示, 
是圓柱的母線, 
是圓柱底面圓的直徑, 
是底面圓周上異于
的任意一點(diǎn), 
.
(1)求證: 
；
(2)求三棱錐
體積的最大值,并寫出此時三棱錐
外接球的表面積.
【答案】(1)見解析；(2) 
.
【解析】試題分析：（1）由圓柱易知
平面
，所以
，由圓的性質(zhì)易得
，進(jìn)而可證
平面
；
（2）由已知得三棱錐
的高
,當(dāng)直角
的面積最大時,三棱錐
的體積最大,當(dāng)點(diǎn)
在弧
中點(diǎn)時
最大, 此時外接球的直徑
即可得解.
試題解析：
(1)證明:∵已知
是圓柱的母線,.∴
平面
∵
是圓柱底面圓的直徑, 
是底面圓周上異于
的任意一點(diǎn),
∴
,又
,∴
平面
又
平面
(2)解:由已知得三棱錐
的高
,當(dāng)直角
的面積最大時,
三棱錐
的體積最大,當(dāng)點(diǎn)
在弧
中點(diǎn)時
最大,
,
結(jié)合(1)可得三棱錐
的外接球的直徑即為
,
所以此時外接球的直徑
.
.
口算題卡加應(yīng)用題集訓(xùn)系列答案
綜合自測系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦！ | 初一 | 初一免費(fèi)課程推薦！ |
| 高二 | 高二免費(fèi)課程推薦！ | 初二 | 初二免費(fèi)課程推薦！ |
| 高三 | 高三免費(fèi)課程推薦！ | 初三 | 初三免費(fèi)課程推薦！ |
科目：高中數(shù)學(xué) 來源： 題型：
【題目】某校為了解1000名高一新生的身體生長狀況，用系統(tǒng)抽樣法（按等距的規(guī)則）抽取40名同學(xué)進(jìn)行檢查，將學(xué)生從1～1000進(jìn)行編號，現(xiàn)已知第18組抽取的號碼為443，則第一組用簡單隨機(jī)抽樣抽取的號碼為 ．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】在三棱柱ABC﹣A1B1C1中，側(cè)面ABB1A1為矩形，AB=2，AA1=2 
，D是AA1的中點(diǎn)，BD與AB1交于點(diǎn)O，且CO⊥平面ABB1A1 ．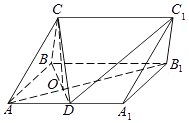 
（1）證明：CD⊥AB1；
（2）若OC=OA，求直線CD與平面ABC所成角的正弦值．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
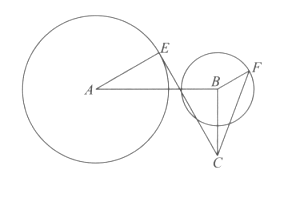
【題目】如圖，已知AB⊥BC，AB=
BC=
a，a∈[1，3]，圓A是以A為圓心、半徑為2的圓，圓B是以B為圓心、半徑為1的圓，設(shè)點(diǎn)E、F分別為圓A、圓B上的動點(diǎn)， 
∥
（且
與
同向），設(shè)∠BAE=θ(θ∈[0，π])．
(I)當(dāng)a= 
，且θ=
時，求
的值；
(Ⅱ)用a，θ表示出
，并給出一組a，θ的值，使得
最小．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】如圖所示，在棱長為4的正方體ABCD﹣A1B1C1D1中，點(diǎn)E是棱CC1的中點(diǎn)，則異面直線D1E與AC所成角的余弦值是 ． 
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知E，F(xiàn)分別是棱長為1的正方體ABCD﹣A1B1C1D1的棱BC，CC1的中點(diǎn)，則截面AEFD1與底面ABCD所成二面角的正弦值是 ．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】設(shè)函數(shù)f（x）=ex（sinx﹣cosx）（0≤x≤2016π），則函數(shù)f（x）的各極大值之和為（ ）
A.
B.
C.
D.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知拋物線 
，焦點(diǎn)到準(zhǔn)線的距離為4，過點(diǎn) 
的直線交拋物線于 
兩點(diǎn)．
（Ⅰ）求拋物線的方程；
（Ⅱ）如果點(diǎn) 
恰是線段 
的中點(diǎn)，求直線 的方程．
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
