
【題目】在△ABC中,角A、B,C所對的邊為a,b,c,若 ![]()
(1)求角B的值;
(2)求△ABC的面積.
【答案】
(1)解:∵a=2 ![]() ,b=6,A=30°,
,b=6,A=30°,
∴由正弦定理 ![]() =
= ![]() 得:sinB=
得:sinB= ![]() =
= ![]() =
= ![]() ,
,
∵a<b,∴A<B,
∴B=60°或B=120°;
(2)解:當B=60°時,C=180°﹣30°﹣60°=90°,
∴S△ABC= ![]() ab=
ab= ![]() ×2
×2 ![]() ×6=6
×6=6 ![]() ;
;
當B=120°時,C=180°﹣30°﹣120°=30°,
∴S△ABC= ![]() absinC=
absinC= ![]() ×2
×2 ![]() ×6×
×6× ![]() =3
=3 ![]() .
.
【解析】(1)由A的度數求出sinA的值,再由a與b的長,利用正弦定理求出sinB的值,由a小于b,得到A小于B,利用特殊角的三角函數值即可求出B的度數;(2)由A與B的度數,利用三角形的內角和定理求出C的度數,利用三角形的面積公式即可求出三角形ABC的面積.
【考點精析】本題主要考查了正弦定理的定義的相關知識點,需要掌握正弦定理:![]() 才能正確解答此題.
才能正確解答此題.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】所謂正三棱錐,指的是底面為正三角形,頂點在底面上的射影為底面三角形中心的三棱錐,在正三棱錐S﹣ABC中,M是SC的中點,且AM⊥SB,底面邊長AB=2 ![]() ,則正三棱錐S﹣ABC的體積為 , 其外接球的表面積為 .
,則正三棱錐S﹣ABC的體積為 , 其外接球的表面積為 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】連接球面上兩點的線段稱為球的弦,半徑為4的球的兩條弦AB、CD的長度分別為2 ![]() 和4
和4 ![]() ,M、N分別是AB、CD的中點,兩條弦的兩端都在球面上運動,有下面四個命題:
,M、N分別是AB、CD的中點,兩條弦的兩端都在球面上運動,有下面四個命題:
①弦AB、CD可能相交于點M;
②弦AB、CD可能相交于點N;
③MN的最大值是5;
④MN的最小值是1;
其中所有正確命題的序號為 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知幾何體A﹣BCED的三視圖如圖所示,其中俯視圖和側視圖都是腰長為4的等腰直角三角形,正視圖為直角梯形. 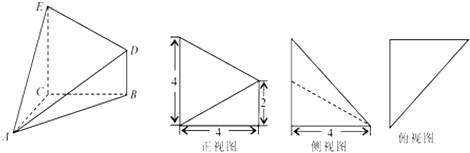
(1)求此幾何體的體積V的大小;
(2)求異面直線DE與AB所成角的余弦值;
(3)求二面角A﹣ED﹣B的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】阿海準備購買“海馬”牌一輛小汽車,其中購車費用12.8萬元,每年的保險費、汽油費約為0.95萬元,年維修、保養費第一年是0.1萬元,以后逐年遞增0.1萬元.請你幫阿海計算一下這種汽車使用多少年,它的年平均費用最少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設不等式組 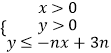 所表示的平面區域為Dn , 記Dn內的格點(格點即橫坐標和縱坐標皆為整數的點)的個數為f(n)(n∈N*).
所表示的平面區域為Dn , 記Dn內的格點(格點即橫坐標和縱坐標皆為整數的點)的個數為f(n)(n∈N*).
(1)求f(1)、f(2)的值及f(n)的表達式;
(2)設bn=2nf(n),Sn為{bn}的前n項和,求Sn;
(3)記 ![]() ,若對于一切正整數n,總有Tn≤m成立,求實數m的取值范圍.
,若對于一切正整數n,總有Tn≤m成立,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在直三棱柱ABC﹣A1B1C1中,D,E分別為AB,BC的中點,點F在側棱B1B上,且B1D⊥A1F,A1C1⊥A1B1 . 求證: 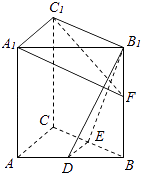
(1)直線DE∥平面A1C1F;
(2)平面B1DE⊥平面A1C1F.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-5:不等式選講
定義在![]() 上的函數
上的函數![]() ,若
,若![]() ,有
,有![]() ,則稱函數
,則稱函數![]() 為定義在
為定義在![]() 上的非嚴格單增函數;若
上的非嚴格單增函數;若![]() ,有
,有![]() ,則稱函數
,則稱函數![]() 為定義在
為定義在![]() 上的非嚴格單減函數.已知:
上的非嚴格單減函數.已知: ![]() .
.
(1)若函數![]() 為定義在
為定義在![]() 上的非嚴格單增函數,求實數
上的非嚴格單增函數,求實數![]() 的取值范圍.
的取值范圍.
(2)若函數![]() 為定義在
為定義在![]() 上的非嚴格單減函數,試解不等式
上的非嚴格單減函數,試解不等式![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com