
【題目】在矩形![]() 中,
中, ![]() 動點(diǎn)
動點(diǎn)![]() 在以點(diǎn)
在以點(diǎn)![]() 為圓心且與
為圓心且與![]() 相切的圓上,若
相切的圓上,若![]() ,則
,則![]() 的最大值為( )
的最大值為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】如圖:以A為原點(diǎn),以AB,AD所在的直線為x,y軸建立如圖所示的坐標(biāo)系,
則A(0,0),B(1,0),D(0,2),C(1,2),
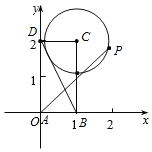
∵動點(diǎn)P在以點(diǎn)C為圓心且與BD相切的圓上,
設(shè)圓的半徑為r,
∵BC=2,CD=1,
∴BD=![]() =
=![]()
∴![]() BCCD=
BCCD=![]() BDr,
BDr,
∴r=![]() ,
,
∴圓的方程為(x﹣1)2+(y﹣2)2=![]() ,
,
設(shè)點(diǎn)P的坐標(biāo)為(![]() cosθ+1,
cosθ+1, ![]() sinθ+2),
sinθ+2),
∵![]() ,
,
∴(![]() cosθ+1,
cosθ+1, ![]() sinθ+2)=λ(1,0)+μ(0,2)=(λ,2μ),
sinθ+2)=λ(1,0)+μ(0,2)=(λ,2μ),
∴![]() cosθ+1=λ,
cosθ+1=λ, ![]() sinθ+2=2μ,
sinθ+2=2μ,
∴λ+μ=![]() cosθ+
cosθ+![]() sinθ+2=sin(θ+φ)+2,其中tanφ=2,
sinθ+2=sin(θ+φ)+2,其中tanφ=2,
∵﹣1≤sin(θ+φ)≤1,
∴1≤λ+μ≤3,
故λ+μ的最大值為3,
故選:A


 53隨堂測系列答案
53隨堂測系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某校從高一年級學(xué)生中隨機(jī)抽取40中學(xué)生,將他們的期中考試數(shù)學(xué)成績(滿分100分,成績均為不低于40分的整數(shù))分成六段: ![]() ,
, ![]() ,…,
,…, ![]() 所得到如圖所示的頻率分布直方圖.
所得到如圖所示的頻率分布直方圖.

(1)求圖中實(shí)數(shù)![]() 的值;
的值;
(2)若該校高一年級共有640人,試估計(jì)該校高一年級期中考試數(shù)學(xué)成績不低于60分的人數(shù);
(3)若從數(shù)學(xué)成績在![]() 與
與![]() 兩個分?jǐn)?shù)段內(nèi)的學(xué)生中隨機(jī)選取2名學(xué)生,求這2名學(xué)生的數(shù)學(xué)成績之差的絕對值不大于10的概率.
兩個分?jǐn)?shù)段內(nèi)的學(xué)生中隨機(jī)選取2名學(xué)生,求這2名學(xué)生的數(shù)學(xué)成績之差的絕對值不大于10的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】下圖是一個求20個數(shù)的平均數(shù)的程序,在橫線上應(yīng)填 ( )
A.i>20
B.i<20
C.i>=20
D.i<=20
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知左、右焦點(diǎn)分別為![]() 的橢圓
的橢圓![]() 與直線
與直線![]() 相交于
相交于![]() 兩點(diǎn),使得四邊形
兩點(diǎn),使得四邊形![]() 為面積等于
為面積等于![]() 的矩形.
的矩形.
(1)求橢圓![]() 的方程;
的方程;
(2)過橢圓![]() 上一動點(diǎn)
上一動點(diǎn)![]() (不在
(不在![]() 軸上)作圓
軸上)作圓![]() 的兩條切線
的兩條切線![]() ,切點(diǎn)分別為
,切點(diǎn)分別為![]() ,直線
,直線![]() 與橢圓
與橢圓![]() 交于
交于![]() 兩點(diǎn),
兩點(diǎn), ![]() 為坐標(biāo)原點(diǎn),求
為坐標(biāo)原點(diǎn),求![]() 的面積
的面積![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,長方體ABCD﹣A1B1C1D1中,AB=AD=1,AA1=2,點(diǎn)P為DD1的中點(diǎn). 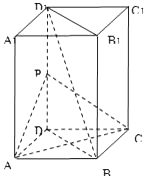
(1)求證:直線BD1∥平面PAC;
(2)求證:平面PAC⊥平面BDD1B1;
(3)求CP與平面BDD1B1所成的角大小.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在△ABC中,內(nèi)角A,B,C的對邊分別為a,b,c,且bsinA= ![]() acosB.
acosB.
(1)求角B的大小;
(2)若b=3,sinC=2sinA,分別求a和c的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】選修4一5:不等式選講.
已知函數(shù)![]() .
.
(1)求![]() 的解集;
的解集;
(2)設(shè)函數(shù)![]() ,若
,若![]() 對任意的
對任意的![]() 都成立,求實(shí)數(shù)
都成立,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com