【題目】在
中，角
、
、
所對的邊分別為
、
、
，
.
（1）若
，求
的值；
（2）若
，求的面積的最大值.
【答案】（1）2；（2）
.
【解析】
（1）由已知利用同角三角函數(shù)基本關(guān)系式可求sinA，sinB的值，利用正弦定理即可得解；
（2）由余弦定理，基本不等式可求bc
，進而根據(jù)三角形面積公式即可計算得解．
解：（1）∵在△ABC中，角A、B、C所對的邊分別為a、b、c，cosA
，cosB
，
∴sinA
，sinB
，
∴由正弦定理可得：
2．
（2）∵a
，cosA．sinA
，
∴由余弦定理a2＝b2+c2﹣2bccosA，可得：3＝b2+c2
bc≥2bcbc
bc，可得：bc，當(dāng)且僅當(dāng)b＝c時等號成立，
∴S△ABC
bcsinA
，當(dāng)且僅當(dāng)b＝c時等號成立，
∴△ABC的面積的最大值
．
黎明文化寒假作業(yè)系列答案科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知數(shù)列
滿足
.
（1）證明：數(shù)列為等差數(shù)列；
（2）設(shè)數(shù)列的前n項和為
，若
，且對任意的正整數(shù)n，都有
，求整數(shù)
的值；
（3）設(shè)數(shù)列
滿足
，若
，且存在正整數(shù)s，t，使得
是整數(shù)，求
的最小值.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
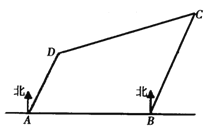
【題目】如圖，有四座城市
、
、
、
，其中在的正東方向，且與相距
，在的北偏東
方向，且與相距
；在的北偏東方向，且與相距
，一架飛機從城市出發(fā)以
的速度向城市飛行，飛行了
，接到命令改變航向，飛向城市，此時飛機距離城市有（ ）
A.B.
C.
D.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】.已知函數(shù)
，
.
（1）當(dāng)
時，求曲線
在點
處的切線方程；
（2）當(dāng)
時，求證：函數(shù)
恰有兩個零點.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】設(shè)函數(shù)
、
的定義域均為
，若對任意
，且
，具有
，則稱函數(shù)為上的單調(diào)非減函數(shù)，給出以下命題：① 若關(guān)于點
和直線
（
）對稱，則為周期函數(shù)，且
是的一個周期；② 若是周期函數(shù)，且關(guān)于直線
對稱，則必關(guān)于無窮多條直線對稱；③ 若是單調(diào)非減函數(shù)，且關(guān)于無窮多個點中心對稱，則的圖象是一條直線；④ 若是單調(diào)非減函數(shù)，且關(guān)于無窮多條平行于
軸的直線對稱，則是常值函數(shù)；以上命題中，所有真命題的序號是_________
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知三棱錐
如圖
的展開圖如圖2,其中四邊形ABCD為邊長等于
的正方形,
和
均為正三角形．
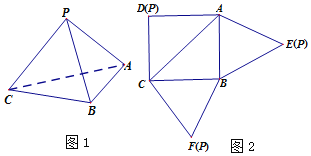
(1)證明：平面
平面ABC；
(2)若M是PC的中點,點N在線段PA上,且滿足
,求直線MN與平面PAB所成角的正弦值．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知函數(shù)
，定義函數(shù)
，給出下列命題：①
；②函數(shù)
是奇函數(shù)；③當(dāng)
時，若
，
，總有
成立，其中所有正確命題的序號是（ ）
A.②B.①②C.③D.②③
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知曲線
的極坐標(biāo)方程為
，以極點
為原點，極軸所在直線為
軸建立直角坐標(biāo)系.過點
作傾斜角為
的直線
交曲線于
，
兩點.
（1）求曲線的直角坐標(biāo)方程，并寫出直線的參數(shù)方程；
（2）過點的另一條直線
與關(guān)于直線
對稱，且與曲線交于
，
兩點，求證：
.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
