
【題目】已知函數f(x)=ex+ax,(a∈R),其圖象與x軸交于A(x1 , 0),B(x2 , 0)兩點,且x1<x2
(1)求a的取值范圍;
(2)證明: ![]() ;(f′(x)為f(x)的導函數)
;(f′(x)為f(x)的導函數)
(3)設點C在函數f(x)的圖象上,且△ABC為等邊三角形,記 ![]() ,求(t﹣1)(a+
,求(t﹣1)(a+ ![]() )的值.
)的值.
【答案】
(1)解:∵f(x)=ex+ax,∴f'(x)=ex+a,
若a≥0,則f'(x)>0,則函數f(x)在R上單調遞增,這與題設矛盾.
∴a<0,
令f′(x)>0得x>ln(﹣a),令f′(x)<0得x<ln(﹣a),
∴f(x)在(﹣∞,ln(﹣a))上單調遞減,在(ln(﹣a),+∞)上單調遞增,
∴f(x)有兩個零點,
∴fmin(x)=f(ln(﹣a))=﹣a+aln(﹣a),
∴﹣a+aln(﹣a)<0,解得a<﹣e.
(2)解:證明:∵x1,x2是f(x)的零點,∴ 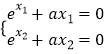 ,
,
兩式相減得:a=﹣ ![]() .
.
記 ![]() =s,則f′(
=s,則f′( ![]() )=e
)=e ![]() ﹣
﹣ ![]() =
= ![]() [2s﹣(es﹣e﹣s)],
[2s﹣(es﹣e﹣s)],
設g(s)=2s﹣(es﹣e﹣s),則g′(s)=2﹣(es+e﹣s)<0,
∴g(s)是減函數,
∴g(s)<g(0)=0,
又 ![]() >0,∴f′(
>0,∴f′( ![]() )<0.
)<0.
∵f′(x)=ex+a是增函數,
∴f′( ![]() )<f′(
)<f′( ![]() )<0
)<0
(3)解:由 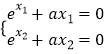 得
得 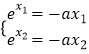 ,∴e
,∴e ![]() =﹣a
=﹣a ![]() ,
,
設P(x0,y0),在等邊三角形ABC中,易知 ![]() ,y0=f(x0)<0,
,y0=f(x0)<0,
由等邊三角形性質知y0=﹣ ![]() ,∴y0+
,∴y0+ ![]() =0,即
=0,即 ![]() ,
,
∴﹣a ![]() +
+ ![]() (x1+x2)+
(x1+x2)+ ![]() =0,
=0,
∵x1>0,∴  ,
,
∴﹣at+ ![]() (t2+1)+
(t2+1)+ ![]() (t2﹣1)=0,即(a+
(t2﹣1)=0,即(a+ ![]() )t2﹣2at+a﹣
)t2﹣2at+a﹣ ![]() =0,
=0,
∴[(a+ ![]() )t+
)t+ ![]() ](t﹣1)=0,
](t﹣1)=0,
∵t>1,∴(a+ ![]() )t+
)t+ ![]() =0,
=0,
∴ ![]() ,
,
∴ ![]() .
.
【解析】(1)討論a的符號,判斷f(x)的單調性,計算f(x)的極值,根據零點個數得出f(x)的極小值為負數,列出不等式解出a;(2)計算f′( ![]() ),根據函數單調性判斷f′(
),根據函數單調性判斷f′( ![]() )的符號,根據f′(x)的單調性得出結論;(3)用x1 , x2表示出P點坐標,根據等邊三角形的性質列方程化簡即可求出t和a的關系,再計算(t﹣1)(a+
)的符號,根據f′(x)的單調性得出結論;(3)用x1 , x2表示出P點坐標,根據等邊三角形的性質列方程化簡即可求出t和a的關系,再計算(t﹣1)(a+ ![]() )的值.
)的值.
【考點精析】認真審題,首先需要了解利用導數研究函數的單調性(一般的,函數的單調性與其導數的正負有如下關系: 在某個區間![]() 內,(1)如果
內,(1)如果![]() ,那么函數
,那么函數![]() 在這個區間單調遞增;(2)如果
在這個區間單調遞增;(2)如果![]() ,那么函數
,那么函數![]() 在這個區間單調遞減).
在這個區間單調遞減).


科目:高中數學 來源: 題型:
【題目】已知![]() ,函數
,函數![]() .
.
(Ⅰ)若![]() ,求函數
,求函數![]() 的值域;
的值域;
(Ⅱ)若函數![]() 在
在![]() 上不單調,求實數
上不單調,求實數![]() 的取值范圍;
的取值范圍;
(Ⅲ)若![]() 是函數
是函數![]() (
(![]() 為實數)的其中兩個零點,且
為實數)的其中兩個零點,且![]() ,求當
,求當![]() 變化時,
變化時, ![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知各項均為正數的數列![]() 滿足
滿足![]() , 且
, 且![]() ,其中
,其中![]() .
.
(1) 求數列![]() 的通項公式;
的通項公式;
(2) 設數列{bn}滿足 bn=![]() ,是否存在正整數
,是否存在正整數![]() ,使得b1,bm,bn成等比數列?若存在,求出所有的
,使得b1,bm,bn成等比數列?若存在,求出所有的![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
(3) 令![]() ,記數列{cn}的前
,記數列{cn}的前![]() 項和為
項和為![]() ,其中
,其中![]() ,證明:
,證明:![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(選修4﹣4:坐標系與參數方程):
在直角坐標系xOy中,以原點O為極點,x軸的正半軸為極軸建立極坐標系,已知射線θ= ![]() 與曲線
與曲線 ![]() (t為參數)相交于A,B來兩點,則線段AB的中點的直角坐標為 .
(t為參數)相交于A,B來兩點,則線段AB的中點的直角坐標為 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某種汽車購買時費用為16.9萬元,每年應交付保險費、汽油費共0.9萬元,汽車的維修保養費為:第一年0.2萬元,第二年0.4萬元,第三年0.6萬元,……依等差數列逐年遞增.
(1)求該車使用了3年的總費用(包括購車費用)為多少萬元?
(2)設該車使用![]() 年的總費用(包括購車費用)為
年的總費用(包括購車費用)為![]() ),試寫出
),試寫出![]() 的表達式;
的表達式;
(3)求這種汽車使用多少年報廢最合算(即該車使用多少年平均費用最少).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐 ![]() 中,
中, ![]() 底面
底面 ![]() ,
, ![]() 是直角梯形,
是直角梯形, ![]() ,
, ![]() ,且
,且 ![]() ,
, ![]() 是
是 ![]() 的中點.
的中點.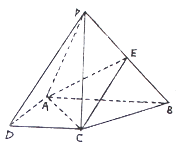
(1)求證:平面 ![]() 平面
平面 ![]() ;
;
(2)若二面角 ![]() 的余弦值為
的余弦值為 ![]() ,求直線
,求直線 ![]() 與平面
與平面 ![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com