
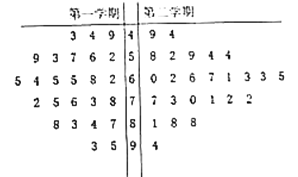
【題目】某學校高二年級的第二學期,因某學科的任課教師王老師調(diào)動工作,于是更換了另一名教師趙老師繼任.第二學期結(jié)束后從全學年的該門課的學生考試成績中用隨機抽樣的方法抽取了容量為50的樣本,用莖葉圖表示如下:
學校秉持均衡發(fā)展、素質(zhì)教育的辦學理念,對教師的教學成績實行績效考核,績效考核方案規(guī)定:每個學期的學生成績中與其中位數(shù)相差在![]() 范圍內(nèi)(含
范圍內(nèi)(含![]() )的為合格,此時相應的給教師賦分為1分;與中位數(shù)之差大于10的為優(yōu)秀,此時相應的給教師賦分為2分;與中位數(shù)之差小于-10的為不合格,此時相應的給教師賦分為-1分.
)的為合格,此時相應的給教師賦分為1分;與中位數(shù)之差大于10的為優(yōu)秀,此時相應的給教師賦分為2分;與中位數(shù)之差小于-10的為不合格,此時相應的給教師賦分為-1分.
(Ⅰ)問王老師和趙老師的教學績效考核平均成績哪個大?
(Ⅱ)是否有![]() 的把握認為“學生成績?nèi)〉脙?yōu)秀與更換老師有關(guān)”.
的把握認為“學生成績?nèi)〉脙?yōu)秀與更換老師有關(guān)”.
附:![]()
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
【答案】(Ⅰ)王老師;(Ⅱ)沒有.
【解析】
(Ⅰ)分別計算王老師和趙老師績效考核的平均成績,進行比較即可;(Ⅱ)完成列聯(lián)表,計算![]() 的值,利用獨立性檢驗的知識進行判斷即可.
的值,利用獨立性檢驗的知識進行判斷即可.
(Ⅰ)第一學期的數(shù)據(jù)為:
43,44,49,52,53,56,57,59,62,64,65,65,65,68,72,73,75,76,78,83,84,87,88,93,95,
其“中位數(shù)”為65,優(yōu)秀有8個,合格有12個,不合格有5個.
∴王老師的教學績效考核平均成績?yōu)椋?/span>![]() ;
;
第二學期的數(shù)據(jù)為:
44,49,52,54,54,58,59,60,61,62,63,63,65,66,67,70,71,72,72,73,77,81,88,88,94,
其“中位數(shù)”為65,優(yōu)秀有5個,合格有15個,不合格有5個,
∴趙老師的教學績效考核平均成績?yōu)椋?/span>![]() ,
,
∴![]() ,所以,王老師的教學績效考核平均成績較大;
,所以,王老師的教學績效考核平均成績較大;
(Ⅱ)由題意得:
第一學期 | 第二學期 | 合計 | |
優(yōu)秀 | 8 | 5 | 13 |
非優(yōu)秀 | 17 | 20 | 37 |
合計 | 25 | 25 | 50 |
![]() ,
,
∵![]() ,∴沒有
,∴沒有![]() 的把握認為“學生成績優(yōu)秀與更換老師有關(guān)”.
的把握認為“學生成績優(yōu)秀與更換老師有關(guān)”.


科目:高中數(shù)學 來源: 題型:
【題目】已知橢圓![]() 的左、右焦點為別為F1、F2,且過點
的左、右焦點為別為F1、F2,且過點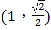 和
和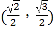 .
.

(1)求橢圓的標準方程;
(2)如圖,點A為橢圓上一位于x軸上方的動點,AF2的延長線與橢圓交于點B,AO的延長線與橢圓交于點C,求△ABC面積的最大值,并寫出取到最大值時直線BC的方程.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某農(nóng)戶計劃種植萵筍和西紅柿,種植面積不超過![]() 畝,投入資金不超過
畝,投入資金不超過![]() 萬元,假設(shè)種植萵筍和西紅柿的產(chǎn)量、成本和售價如下表:
萬元,假設(shè)種植萵筍和西紅柿的產(chǎn)量、成本和售價如下表:
年產(chǎn)量/畝 | 年種植成本/畝 | 每噸售價 | |
萵筍 | 5噸 | 1萬元 | 0.5萬元 |
西紅柿 | 4.5噸 | 0.5萬元 | 0.4萬元 |
那么,該農(nóng)戶一年種植總利潤(總利潤=總銷售收入-總種植成本)的最大值為____萬元
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】為發(fā)展業(yè)務,某調(diào)研組對![]() ,
,![]() 兩個公司的產(chǎn)品需求量進行調(diào)研,準備從國內(nèi)
兩個公司的產(chǎn)品需求量進行調(diào)研,準備從國內(nèi)![]() 個人口超過
個人口超過![]() 萬的超大城市和
萬的超大城市和![]() (
(![]() )個人口低于
)個人口低于![]() 萬的小城市隨機抽取若干個進行統(tǒng)計,若一次抽取
萬的小城市隨機抽取若干個進行統(tǒng)計,若一次抽取![]() 個城市,全是小城市的概率為
個城市,全是小城市的概率為![]() .
.
(1)求![]() 的值;
的值;
(2)若一次抽取![]() 個城市,則:①假設(shè)取出小城市的個數(shù)為
個城市,則:①假設(shè)取出小城市的個數(shù)為![]() ,求
,求![]() 的分布列和期望;
的分布列和期望;
②若取出的![]() 個城市是同一類城市,求全為超大城市的概率.
個城市是同一類城市,求全為超大城市的概率.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知![]() ,
,![]() 是函數(shù)
是函數(shù)![]() (其中常數(shù)
(其中常數(shù)![]() )圖象上的兩個動點,點
)圖象上的兩個動點,點![]() ,若
,若![]() 的最小值為0,則函數(shù)
的最小值為0,則函數(shù)![]() 的最大值為__________.
的最大值為__________.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在平面直角坐標系![]() 中,曲線
中,曲線![]() 的參數(shù)方程是
的參數(shù)方程是![]() (
(![]() 為參數(shù)),以原點
為參數(shù)),以原點![]() 為極點,
為極點, ![]() 軸正半軸為極軸,建立極坐標系,直線
軸正半軸為極軸,建立極坐標系,直線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(Ⅰ)求曲線![]() 的普通方程與直線
的普通方程與直線![]() 的直角坐標方程;
的直角坐標方程;
(Ⅱ)已知直線![]() 與曲線
與曲線![]() 交于
交于![]() ,
, ![]() 兩點,與
兩點,與![]() 軸交于點
軸交于點![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知兩個平面垂直,下列命題
①一個平面內(nèi)已知直線必垂直于另一個平面內(nèi)的任意一條直線
②一個平面內(nèi)的已知直線必垂直于另一個平面的無數(shù)條直線
③一個平面內(nèi)的任一條直線必垂直于另一個平面
④過一個平面內(nèi)任意一點作交線的垂線,則此垂線必垂直于另一個平面
其中不正確命題的個數(shù)是( )
A.3B.2C.1D.0
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,在三棱錐![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() 、
、![]() 均為等邊三角形,
均為等邊三角形,![]() 為
為![]() 的中點,點
的中點,點![]() 在
在![]() 上.
上.
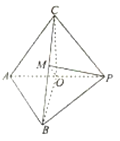
(1)求證:平面![]() 平面
平面![]() ;
;
(2)若點![]() 是線段
是線段![]() 的中點,求直線
的中點,求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】設(shè)函數(shù)![]() .
.
(1)若![]() ,
,![]() ,求函數(shù)
,求函數(shù)![]() 的極值;
的極值;
(2)若![]() 是函數(shù)
是函數(shù)![]() 的一個極值點,試求出
的一個極值點,試求出![]() 關(guān)于
關(guān)于![]() 的關(guān)系式(即用
的關(guān)系式(即用![]() 表示
表示![]() ),并確定
),并確定![]() 的單調(diào)區(qū)間;(提示:應注意對
的單調(diào)區(qū)間;(提示:應注意對![]() 的取值范圍進行討論)
的取值范圍進行討論)
(3)在(2)的條件下,設(shè)![]() ,函數(shù)
,函數(shù)![]() ,若存在
,若存在![]() 使得
使得![]() 成立,求
成立,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com