【題目】如圖放置的邊長(zhǎng)為1的正方形
沿
軸順時(shí)針滾動(dòng)一周，設(shè)頂點(diǎn)
的運(yùn)動(dòng)軌跡與軸所圍區(qū)域?yàn)?/span>
，若在平面區(qū)域
內(nèi)任意取一點(diǎn)
，則所取的點(diǎn)恰好落在區(qū)域內(nèi)部的概率為
A. 
B. 
C. 
D. 
【答案】C
【解析】
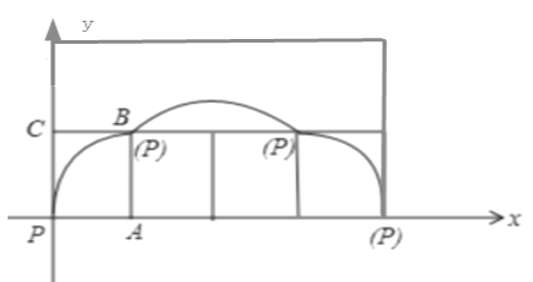
頂點(diǎn)
的運(yùn)動(dòng)軌跡，分三部分：前一部分的圖象為四分之一圓周，后一部分的圖象為四分之一圓周，且半徑都是1,中間部分的軌跡為以
為半徑的四分之一圓周，分別求出與
軸圍成的面積，求和后利用幾何概型概率公式求解即可.
正方形
沿軸順時(shí)針滾動(dòng)一周，頂點(diǎn)的運(yùn)動(dòng)軌跡，分三部分：前一部分的圖象為四分之一圓周，后一部分的圖象為四分之一圓周，且半徑都是1,此時(shí)兩部分扇形所占面積為
,中間部分的軌跡為以為四分之一圓周，與圍成的面積為
,頂點(diǎn)的運(yùn)動(dòng)軌跡與軸所圍區(qū)域
的面積為
，
平面區(qū)域
的面積為
，
所以在平面區(qū)域內(nèi)任意取一點(diǎn)
，
則所取的點(diǎn)恰好落在區(qū)域內(nèi)部的概率為
故選C.
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦！ | 初一 | 初一免費(fèi)課程推薦！ |
| 高二 | 高二免費(fèi)課程推薦！ | 初二 | 初二免費(fèi)課程推薦！ |
| 高三 | 高三免費(fèi)課程推薦！ | 初三 | 初三免費(fèi)課程推薦！ |
科目：高中數(shù)學(xué) 來源： 題型：
【題目】某家庭進(jìn)行理財(cái)投資，根據(jù)長(zhǎng)期收益率市場(chǎng)預(yù)測(cè)，投資債券等穩(wěn)健型產(chǎn)品的年收益
與投資額
成正比，其關(guān)系如圖1；投資股票等風(fēng)險(xiǎn)型產(chǎn)品的年收益
與投資額的算術(shù)平方根成正比，其關(guān)系如圖2.
（1）分別寫出兩種產(chǎn)品的年收益和的函數(shù)關(guān)系式；
（2）該家庭現(xiàn)有20萬元資金，全部用于理財(cái)投資，問:怎么分配資金能使投資獲得最大年收益，其最大年收益是多少萬元?
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】下列說法中，正確的有_______.(寫出所有正確說法的序號(hào))
①在
中，若
，則
；
②在中，若
，則是銳角三角形；
③在中，若
，則
；
④若
是等差數(shù)列，其前
項(xiàng)和為
，則三點(diǎn)
共線；
⑤等比數(shù)列的前項(xiàng)和為，若對(duì)任意的
，點(diǎn)
均在函數(shù)
(
且
，
均為常數(shù))的圖象上，則的值為
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】下面結(jié)論中，正確結(jié)論的是（ ）
A.存在兩個(gè)不等實(shí)數(shù)
，使得等式
成立
B.
(0< x < π)的最小值為4
C.若
是等比數(shù)列
的前
項(xiàng)的和，則
成等比數(shù)列
D.已知
的三個(gè)內(nèi)角
所對(duì)的邊分別為
，若
，則一定是銳角三角形
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】某商場(chǎng)經(jīng)銷某商品，根據(jù)以往資料統(tǒng)計(jì)，顧客采用的付款期數(shù)
的分布列為
| 1 | 2 | 3 | 4 | 5 |
| 0.2 | 0.3 | 0.3 | 0.1 | 0.1 |
商場(chǎng)經(jīng)銷一件該商品，采用1期付款，其利潤(rùn)為200元；分2期或3期付款，其利潤(rùn)為300元；分4期或5期付款，其利潤(rùn)為400元，
表示經(jīng)銷一件該商品的利潤(rùn).
（1）求事件
：“購(gòu)買該商品的3位顧客中，至少有1位采用期付款”的概率
；
（2）求的分布列、期望和方差.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】在
中，已知A，a，b，給出下列說法：
①若
，則此三角形最多有一解；
②若
，且
，則此三角形為直角三角形，且
；
③當(dāng)，且
時(shí)，此三角形有兩解.
其中正確說法的個(gè)數(shù)為（ ）
A.0B.1C.2D.3
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】為改善居民的生活環(huán)境，政府?dāng)M將一公園進(jìn)行改造擴(kuò)建.已知原公園是直徑為200 m的半圓形，出入口在圓心O處，A為居民小區(qū)，OA的距離為200 m，按照設(shè)計(jì)要求，以居民小區(qū)A和圓弧上點(diǎn)B的連線為一條邊向半圓外作等腰直角三角形ABC（C為直角頂點(diǎn)），使改造后的公園如圖中四邊形OACB所示.
（1）若
，則C與出入口O之間的距離為多少米？
（2）
的大小為多少時(shí)，公園OACB的面積最大？
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】在平面直角坐標(biāo)系
中,已知直線
的參數(shù)方程為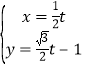
（
為參數(shù)）.在以坐標(biāo)原點(diǎn)
為極點(diǎn),
軸的正半軸為極軸,且與直角坐標(biāo)系長(zhǎng)度單位相同的極坐標(biāo)系中,曲線
的極坐標(biāo)方程是
.
（1）求直線的普通方程與曲線的直角坐標(biāo)方程；
（2）設(shè)點(diǎn)
.若直與曲線相交于兩點(diǎn)
,求
的值.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知
，
的線性回歸直線方程為
，且，之間的一組相關(guān)數(shù)據(jù)如下表所示，則下列說法錯(cuò)誤的為
A.變量，之間呈現(xiàn)正相關(guān)關(guān)系B.可以預(yù)測(cè)，當(dāng)
時(shí)，
C.
D.由表格數(shù)據(jù)可知，該回歸直線必過點(diǎn)
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話：027-86699610 舉報(bào)郵箱：58377363@163.com