
【題目】已知橢圓![]() 的右焦點為
的右焦點為![]() ,上頂點為
,上頂點為![]() ,直線
,直線![]() 與直線
與直線![]() 垂直,橢圓
垂直,橢圓![]() 經過點
經過點![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)過點![]() 作橢圓
作橢圓![]() 的兩條互相垂直的弦
的兩條互相垂直的弦![]() .若弦
.若弦![]() 的中點分別為
的中點分別為![]() ,證明:直線
,證明:直線![]() 恒過定點.
恒過定點.
【答案】(1)![]() ;(2)直線
;(2)直線![]() 經過定點
經過定點![]() .
.
【解析】試題分析:
(1)根據直線![]() 與直線
與直線![]() 垂直可得
垂直可得![]() ,從而得到
,從而得到![]() ,再由點
,再由點![]() 在橢圓上可求得
在橢圓上可求得![]() ,即可得橢圓的方程.(2)當直線
,即可得橢圓的方程.(2)當直線![]() 的斜率都存在時,設
的斜率都存在時,設![]() 的方程為
的方程為![]() ,與橢圓方程聯立消元后根據根據系數的關系可得點
,與橢圓方程聯立消元后根據根據系數的關系可得點![]() 的坐標,同理可得點
的坐標,同理可得點![]() 坐標,從而可得直線
坐標,從而可得直線![]() 的方程,通過此方程可得直線過定點
的方程,通過此方程可得直線過定點![]() .然后再驗證當直線
.然后再驗證當直線![]() 的斜率不存在時也過該定點.
的斜率不存在時也過該定點.
試題解析:
(1)因為直線![]() 與直線
與直線![]() 垂直,
垂直,
所以![]() (
(![]() 為坐標原點),
為坐標原點),
即![]() ,
,
所以![]() .
.
因為點![]() 在橢圓
在橢圓![]() 上,所以
上,所以![]() ,
,
由 ,解得
,解得![]() ,
,
所以橢圓![]() 的標準方程為
的標準方程為![]() .
.
(2)①當直線![]() 的斜率都存在時,
的斜率都存在時,
設直線![]() 的方程為
的方程為![]() ,
,
則直線![]() 的方程為
的方程為![]() ,
,
由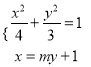 消去x整理得
消去x整理得![]() ,
,
設![]() ,
,
則![]() ,
,
由中點坐標公式得![]() ,
,
用![]() 代替點M坐標中的
代替點M坐標中的![]() 可得
可得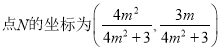 .
.
所以直線![]() 的方程為
的方程為![]() ,
,
令![]() ,得
,得![]() ,
,
所以直線![]() 經過定點
經過定點![]() .
.
②當直線![]() 或
或![]() 的斜率不存在時,可知直線
的斜率不存在時,可知直線![]() 為
為![]() 軸,也經過定點
軸,也經過定點![]() .
.
綜上所述,直線![]() 經過定點
經過定點![]() .
.


科目:高中數學 來源: 題型:
【題目】在標準溫度和大氣壓下,人體血液中氫離子的物質的量的濃度(單位mol/L,記作![]() )和氫氧根離子的物質的量的濃度(單位mol/L,記作
)和氫氧根離子的物質的量的濃度(單位mol/L,記作![]() )的乘積等于常數
)的乘積等于常數![]() .已知pH值的定義為
.已知pH值的定義為![]() ,健康人體血液的pH值保持在7.35~7.45之間,那么健康人體血液中的
,健康人體血液的pH值保持在7.35~7.45之間,那么健康人體血液中的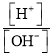 可以為(參考數據:
可以為(參考數據: ![]() ,
, ![]() )
)
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校為了鼓勵學生熱心公益,服務社會,成立了“慈善義工社”.2017年12月,該校“慈善義工社”為學生提供了4次參加公益活動的機會,學生可通過網路平臺報名參加活動.為了解學生實際參加這4次活動的情況,該校隨機抽取100名學生進行調查,數據統計如下表,其中“√”表示參加,“×”表示未參加.
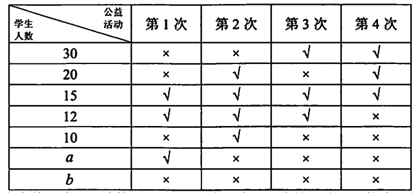
根據表中數據估計,該校4000名學生中約有120名這4次活動均未參加.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)從該校4000名學生中任取一人,試估計其2017年12月恰參加了2次學校組織的公益活動的概率;
(Ⅲ)已知學生每次參加公益活動可獲得10個公益積分,任取該校一名學生,記該生2017年12月獲得的公益積分為![]() ,求隨機變量
,求隨機變量![]() 的分布列和數學期望
的分布列和數學期望![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若函數f(x)=sin2ax-![]() sin ax·cos ax-
sin ax·cos ax-![]() (a>0)的圖象與直線y=b相切,并且切點的橫坐標依次成公差為
(a>0)的圖象與直線y=b相切,并且切點的橫坐標依次成公差為![]() 的等差數列.
的等差數列.
(1)求a,b的值;
(2)若x0∈![]() ,且x0是y=f(x)的零點,試寫出函數y=f(x)在
,且x0是y=f(x)的零點,試寫出函數y=f(x)在![]() 上的單調增區間.
上的單調增區間.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】定義在[1,+∞)上的函數f(x)滿足:①f(2x)=2f(x);②當2≤x≤4時,f(x)=1-|x-3|.則函數g(x)=f(x)-2在區間[1,28]上的零點個數為________.
查看答案和解析>>
科目:高中數學 來源: 題型:
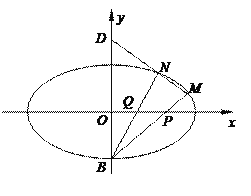
【題目】如圖,在平面直角坐標系![]() 中,橢圓
中,橢圓![]() 的下頂點為
的下頂點為![]() ,點
,點![]() 是橢圓上異于點
是橢圓上異于點![]() 的動點,直線
的動點,直線![]() 分別與
分別與![]() 軸交于點
軸交于點![]() ,且點
,且點![]() 是線段
是線段![]() 的中點.當點
的中點.當點![]() 運動到點
運動到點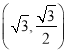 處時,點
處時,點![]() 的坐標為
的坐標為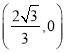 .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)設直線![]() 交
交![]() 軸于點
軸于點![]() ,當點
,當點![]() 均在
均在![]() 軸右側,且
軸右側,且![]() 時,求直線
時,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖1, 在直角梯形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 為線段
為線段![]() 的中點. 將
的中點. 將![]() 沿
沿![]() 折起,使平面
折起,使平面![]()
![]() 平面
平面![]() ,得到幾何體
,得到幾何體![]() ,如圖2所示.
,如圖2所示.
(1)求證: ![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com