
【題目】某制造廠商10月份生產了一批乒乓球,從中隨機抽取![]() 個進行檢查,測得每個球的直徑(單位:
個進行檢查,測得每個球的直徑(單位:![]() ),將數據進行分組,得到如下頻率分布表:
),將數據進行分組,得到如下頻率分布表:

(1)求![]() 、
、![]() 、
、![]() 及
及![]() 、
、![]() 的值,并畫出頻率分布直方圖(結果保留兩位小數);
的值,并畫出頻率分布直方圖(結果保留兩位小數);
(2)已知標準乒乓球的直徑為![]() ,直徑誤差不超過
,直徑誤差不超過![]() 的為五星乒乓球,若這批乒乓球共有
的為五星乒乓球,若這批乒乓球共有![]() 個,試估計其中五星乒乓球的數目;
個,試估計其中五星乒乓球的數目;
(3)統計方法中,同一組數據常用該組區間的中點值(例如區間![]() 的中點值是
的中點值是![]() )作為代表,估計這批乒乓球直徑的平均值和中位數.
)作為代表,估計這批乒乓球直徑的平均值和中位數.
【答案】(1)![]() ,頻率分布直方圖見解析;(2)
,頻率分布直方圖見解析;(2)![]() ;(3)
;(3)![]() ,
,![]() .
.
【解析】試題分析: (1)根據頻率等于頻數除以總數,先求總數![]() ,再求
,再求![]() 對應頻數
對應頻數![]() ,根據頻數和為總數得
,根據頻數和為總數得![]() ,最后再根據頻率等于頻數除以總數,得
,最后再根據頻率等于頻數除以總數,得![]() 、
、![]() 的值,以頻率除以組距作為對應區間縱坐標畫出頻率分布直方圖,(2)直徑在
的值,以頻率除以組距作為對應區間縱坐標畫出頻率分布直方圖,(2)直徑在![]() 內對應概率為
內對應概率為![]() ,根據頻數等于總數乘以頻率,得頻數,(3)由平均值為各組中點值與對應概率乘積的和,得平均值;中位數必在區間
,根據頻數等于總數乘以頻率,得頻數,(3)由平均值為各組中點值與對應概率乘積的和,得平均值;中位數必在區間![]() 內,由頻率關系列等量關系:設中位數為
內,由頻率關系列等量關系:設中位數為![]() ,則有
,則有![]() ,解方程可得中位數.
,解方程可得中位數.
試題解析:(1)由頻率分布表可知![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
頻率分布直方圖如圖:
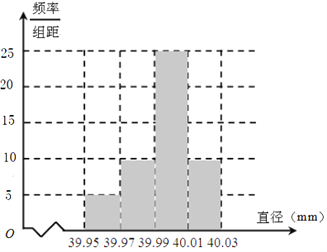
(2)因為五星乒乓球的直徑在![]() 內,所以由頻率分布表,可得五星乒乓球的頻率為
內,所以由頻率分布表,可得五星乒乓球的頻率為![]() ,(6分)
,(6分)
故![]() 個乒乓球中,“五星乒乓球”大約有
個乒乓球中,“五星乒乓球”大約有![]() (個).
(個).
(3)平均數![]() .
.
設中位數為![]() ,則
,則![]() 且
且![]() ,解得
,解得![]() .故中位數為
.故中位數為![]() .
.


 活力課時同步練習冊系列答案
活力課時同步練習冊系列答案科目:高中數學 來源: 題型:
【題目】平面內有兩個定點A(1,0),B(1,﹣2),設點P到A、B的距離分別為![]() ,且
,且![]()
(I)求點P的軌跡C的方程;
(II)是否存在過點A的直線![]() 與軌跡C相交于E、F兩點,滿足
與軌跡C相交于E、F兩點,滿足![]() (O為坐標原點).若存在,求出直線
(O為坐標原點).若存在,求出直線![]() 的方程;若不存在,請說明理由.
的方程;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一盒中裝有除顏色外其余均相同的12個小球,從中隨機取出1個球,取出紅球的概率為![]() ,取出黑球的概率為
,取出黑球的概率為![]() ,取出白球的概率為
,取出白球的概率為![]() ,取出綠球的概率為
,取出綠球的概率為![]() .求:
.求:
(1)取出的1個球是紅球或黑球的概率;
(2)取出的1個球是紅球或黑球或白球的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知等邊![]() 的邊長為4,,
的邊長為4,,![]() 分別為
分別為![]() 邊的中點,
邊的中點,![]() 為
為![]() 的中點,
的中點,![]() 為
為![]() 邊上一點,且
邊上一點,且![]() ,將
,將![]() 沿
沿![]() 折到
折到![]() 的位置,使平面
的位置,使平面![]() 平面
平面![]() .
.

(1)求證:平面![]() 平面
平面![]() ;
;
(2)設![]() ,求三棱錐
,求三棱錐![]() 的體積.
的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙兩人練習罰球,每人練習6組,每組罰球20個,命中個數莖葉圖如下:

(1)求甲命中個數的中位數和乙命中個數的眾數;
(2)通過計算,比較甲乙兩人的罰球水平.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的兩個焦點為
的兩個焦點為![]() ,
,![]() ,離心率為
,離心率為![]() ,點
,點![]() ,
,![]() 在橢圓上,
在橢圓上,![]() 在線段
在線段![]() 上,且
上,且![]() 的周長等于
的周長等于![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)過圓![]() 上任意一點
上任意一點![]() 作橢圓
作橢圓![]() 的兩條切線
的兩條切線![]() 和
和![]() 與圓
與圓![]() 交于點
交于點![]() ,
,![]() ,求
,求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學校一個生物興趣小組對學校的人工湖中養殖的某種魚類進行觀測研究,在飼料充足的前提下,興趣小組對飼養時間x(單位:月)與這種魚類的平均體重y(單位:千克)得到一組觀測值,如下表:
|
|
|
|
|
|
|
|
|
|
|
|
(1)在給出的坐標系中,畫出關于x、y兩個相關變量的散點圖.
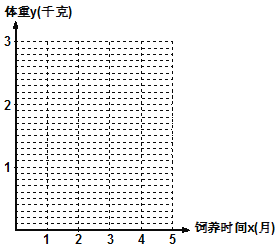
(2)請根據上表提供的數據,用最小二乘法求出變量![]() 關于變量
關于變量![]() 的線性回歸直線方程
的線性回歸直線方程![]() .
.
(3)預測飼養滿12個月時,這種魚的平均體重(單位:千克).
(參考公式: 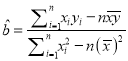 ,
, ![]() )
)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com