
【題目】已知函數![]() ,其定義域為
,其定義域為![]() .(其中常數
.(其中常數![]() ,是自然對數的底數)
,是自然對數的底數)
(1)求函數![]() 的遞增區間;
的遞增區間;
(2)若函數![]() 為定義域上的增函數,且
為定義域上的增函數,且![]() ,證明:
,證明: ![]() .
.
【答案】(1)見解析(2)見解析
【解析】
(1)求得函數的導數![]() ,分類討論,即可求解函數的單調區間;
,分類討論,即可求解函數的單調區間;
(2)由題意,問題轉化為![]() ,令
,令![]() ,
,![]() ,
,
即證![]() ,根據函數的單調性,即可作出證明.
,根據函數的單調性,即可作出證明.
(1)易知![]() ,
,
①若![]() ,由
,由![]() 解得
解得![]() ,∴函數
,∴函數![]() 的遞增區間為
的遞增區間為![]() ;
;
②若![]() ,則
,則
|
|
|
| 1 |
|
| + | 0 | - | 0 | + |
| ↗ | 極大值 | ↘ | 極小值 | ↗ |
∴函數![]() 的遞增區間為
的遞增區間為![]() 和
和![]() ;
;
③若![]() ,則
,則![]() ,∴函數
,∴函數![]() 的遞增區間為
的遞增區間為![]() ;
;
④若![]() ,則
,則
|
| 1 |
|
|
|
| + | 0 | - | 0 | + |
| ↗ | 極大值 | ↘ | 極小值 | ↗ |
∴函數![]() 的遞增區間為
的遞增區間為![]() 和
和![]() ;
;
綜上,若![]() ,
,![]() 的遞增區間為
的遞增區間為![]() ;
;
若![]() ,
,![]() 的遞增區間為
的遞增區間為![]() 和
和![]() ;
;
若![]() ,函數
,函數![]() 的遞增區間為
的遞增區間為![]() ;
;
若![]() ,函數
,函數![]() 的遞增區間為
的遞增區間為![]() 和
和![]() .
.
(2)∵函數![]() 為
為![]() 上的增函數,∴
上的增函數,∴![]() ,即
,即![]() ,
,
注意到![]() ,故
,故![]() ,
,
∴不妨設![]() ,
,
欲證![]() ,只需證
,只需證![]() ,只需證
,只需證![]() ,
,
即證![]() ,即證
,即證![]() ,
,
令![]() ,
,![]() ,只需證
,只需證![]() ,
,
∴![]()
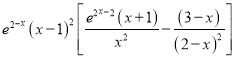 ,
,
下證![]() ,即證
,即證 ,
,
由熟知的不等式![]() 可知
可知![]() ,
,
當![]() 時,即
時,即![]() ,
,
∴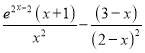
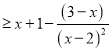
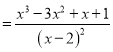 ,
,
易知當![]() 時,
時,![]() ,∴
,∴![]() ,
,
∴ ,
,
∴![]() ,即
,即![]() 單調遞增,即
單調遞增,即![]() ,從而
,從而![]() 得證.
得證.


 學練快車道快樂假期寒假作業系列答案
學練快車道快樂假期寒假作業系列答案 新思維寒假作業系列答案
新思維寒假作業系列答案科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)求函數![]() 的圖象在點
的圖象在點![]() 處的切線方程;
處的切線方程;
(2)若![]() 在
在![]() 上有解,求
上有解,求![]() 的取值范圍;
的取值范圍;
(3)設![]() 是函數
是函數![]() 的導函數,
的導函數,![]() 是函數
是函數![]() 的導函數,若函數
的導函數,若函數![]() 的零點為
的零點為![]() ,則點
,則點![]() 恰好就是該函數
恰好就是該函數![]() 的對稱中心.試求
的對稱中心.試求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數f(x)=x2+acosx+bx,非空數集A={x|f(x)=0},B={x|f(f(x))=0},已知A=B,則參數a的所有取值構成的集合為_____;參數b的所有取值構成的集合為_____.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,四棱錐P﹣ABCD的底面是邊長為2的正方形,平面PAD⊥平面ABCD,PA⊥AD,∠PDA=45°,E,F分別為AB,PC的中點.
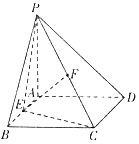
(1)證明:EF∥平面PAD;
(2)在線段BC上是否存在一點H,使平面PAH⊥平面DEF?若存在,求此時二面角C﹣HD﹣P的平面角的正切值:若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知橢圓C:![]() 1(a>b>0)的離心率為
1(a>b>0)的離心率為![]() ,短軸長為2,直線l與圓O:x2+y2
,短軸長為2,直線l與圓O:x2+y2![]() 相切,且與橢圓C相交于M、N兩點.
相切,且與橢圓C相交于M、N兩點.
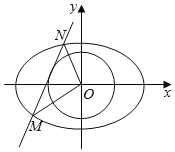
(1)求橢圓C的方程;
(2)證明:![]()
![]() 為定值.
為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() ,
,![]() 為橢圓
為橢圓![]() 的左右焦點,
的左右焦點,![]() 在以
在以![]() 為圓心,1為半徑的圓
為圓心,1為半徑的圓![]() 上,且
上,且![]() .
.
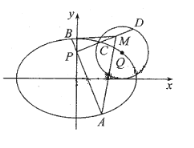
(1)求橢圓![]() 的方程;
的方程;
(2)過點![]() 的直線
的直線![]() 交橢圓
交橢圓![]() 于
于![]() ,
,![]() 兩點,過
兩點,過![]() 與
與![]() 垂直的直線
垂直的直線![]() 交圓
交圓![]() 于
于![]() ,
,![]() 兩點,
兩點,![]() 為線段
為線段![]() 的中點,求
的中點,求![]() 的面積的取值范圍.
的面積的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著新政策的實施,海淘免稅時代于2016年4月8日正式結束,新政策實施后,海外購物的費用可能會增加.為了解新制度對海淘的影響,某記者調查了身邊喜歡海淘的10位朋友,其態度共有兩類:第一類是會降低海淘數量,共有4人,第二類是不會降低海淘數量,共有6人.若該記者計劃從這10人中隨機選取5人按順序進行采訪,則“第一類”的人數多于“第二類”,且采訪中“第二類”不連續進行的不同采訪順序有( )
A.3840B.5040C.6020D.7200
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為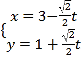 (
(![]() 為參數),在以坐標原點為極點,
為參數),在以坐標原點為極點,![]() 軸正半軸為極軸的極坐標系中,曲線
軸正半軸為極軸的極坐標系中,曲線![]() 的方程為
的方程為![]() .
.
(1)求曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)設曲線![]() 與直線
與直線![]() 交于點
交于點![]() ,點
,點![]() 的坐標為(3,1),求
的坐標為(3,1),求![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com