
【題目】在直角坐標系xOy中,曲線C1的參數方程為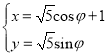 (φ為參數),以坐標原點O為極點,x軸的正半軸為極軸,建立極坐標系.
(φ為參數),以坐標原點O為極點,x軸的正半軸為極軸,建立極坐標系.
(1)求C1的極坐標方程;
(2)若C1與曲線C2:ρ=2sinθ交于A,B兩點,求|OA||OB|的值.
科目:高中數學 來源: 題型:
【題目】給出以下四個命題:
①設![]() 是空間中的三條直線,若
是空間中的三條直線,若![]() ,
,![]() ,則
,則![]() .
.
②在面積為![]() 的
的![]() 的邊
的邊![]() 上任取一點
上任取一點![]() ,則
,則![]() 的面積大于
的面積大于![]() 的概率為
的概率為![]() .
.
③已知一個回歸直線方程為![]()
![]() ,則
,則![]() .
.
④數列![]() 為等差數列的充要條件是其通項公式為
為等差數列的充要條件是其通項公式為![]() 的一次函數.
的一次函數.
其中正確命題的充號為________.(把所有正確命題的序號都填上)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某產品自生產并投入市場以來,生產企業為確保產品質量,決定邀請第三方檢測機構對產品進行質量檢測,并依據質量指標Z來衡量產品的質量.當![]() 時,產品為優等品;當
時,產品為優等品;當![]() 時,產品為一等品;當
時,產品為一等品;當![]() 時,產品為二等品.第三方檢測機構在該產品中隨機抽取500件,繪制了這500件產品的質量指標
時,產品為二等品.第三方檢測機構在該產品中隨機抽取500件,繪制了這500件產品的質量指標![]() 的條形圖.用隨機抽取的500件產品作為樣本,估計該企業生產該產品的質量情況,并用頻率估計概率.
的條形圖.用隨機抽取的500件產品作為樣本,估計該企業生產該產品的質量情況,并用頻率估計概率.
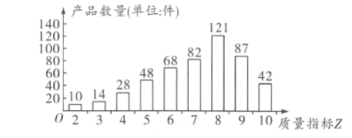
(1)從該企業生產的所有產品中隨機抽取4件,求至少有1件優等品的概率;
(2)現某人決定購買80件該產品.已知每件成本1000元,購買前,邀請第三方檢測機構對要購買的80件產品進行抽樣檢測,買家、企業及第三方檢測機構就檢測方案達成以下協議:從80件產品中隨機抽出4件產品進行檢測,若檢測出3件或4件為優等品,則按每件1600元購買,否則按每件1500元購買,每件產品的檢測費用250元由企業承擔.記企業的收益為X元,求X的分布列與數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系中,曲線C的參數方程為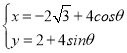 (θ為參數),直線l的參數方程為
(θ為參數),直線l的參數方程為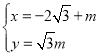 (m為參數),以平面直角坐標系的原點O為極點,x軸正半軸為極軸,建立坐標系.
(m為參數),以平面直角坐標系的原點O為極點,x軸正半軸為極軸,建立坐標系.
(1)求曲線C的極坐標方程;
(2)直線l與曲線C相交于M,N兩點,若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設首項為a1的正項數列{an}的前n項和為Sn,q為非零常數,已知對任意正整數n,m,Sn+m=Sm+qmSn總成立.
(1)求證:數列{an}是等比數列;
(2)若不等的正整數m,k,h成等差數列,試比較ammahh與ak2k的大小;
(3)若不等的正整數m,k,h成等比數列,試比較![]() 與
與![]() 的大小.
的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
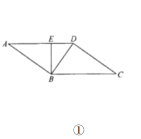
【題目】如圖①:在平行四邊形![]() 中,
中,![]() ,
,![]() ,將
,將![]() 沿對角線
沿對角線![]() 折起,使
折起,使![]() ,連結
,連結![]() ,得到如圖②所示三棱錐
,得到如圖②所示三棱錐![]() .
.
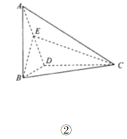
(1)證明:![]() 平面
平面![]() ;
;
(2)若![]() ,二面角
,二面角![]() 的平面角的正切值為
的平面角的正切值為![]() ,求直線
,求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】黨的十九大明確把精準脫貧作為決勝全面建成小康社會必須打好的三大攻堅戰之一,為堅決打贏脫貧攻堅戰,某幫扶單位考察了甲乙兩種不同的農產品加工生產方式,現對兩種生產方式加工的產品質量進行測試并打分對比,得到如下數據:
生產方式甲 | 分值區間 |
|
|
|
|
|
頻數 | 20 | 30 | 100 | 40 | 10 | |
生產方式乙 | 分值區間 |
|
|
|
|
|
頻數 | 25 | 35 | 60 | 50 | 30 |
其中產品質量按測試指標可劃分為:指標在區間![]() 上的為特優品,指標在區間
上的為特優品,指標在區間![]() 上的為一等品,指標在區間
上的為一等品,指標在區間![]() 上的為二等品.
上的為二等品.
(1)用事件![]() 表示“按照生產方式甲生產的產品為特優品”,估計
表示“按照生產方式甲生產的產品為特優品”,估計![]() 的概率;
的概率;
(2)填寫下面列聯表,并根據列聯表判斷能否有![]() 的把握認為“特優品”與生產方式有關?
的把握認為“特優品”與生產方式有關?
特優品 | 非特優品 | |
生產方式甲 | ||
生產方式乙 |
(3)根據打分結果對甲乙兩種生產方式進行優劣比較.
附表:
| 0.10 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
參考公式: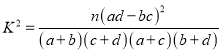 ,其中
,其中![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com