
甲乙兩人進行掰手腕比賽,比賽規則規定三分鐘為一局,三分鐘內不分勝負為平局,當有一人贏3局就結束比賽,否則繼續進行,根據以往經驗,每次甲勝的概率為 ,乙勝的概率為
,乙勝的概率為 ,且每局比賽勝負互不受影響.
,且每局比賽勝負互不受影響.
(Ⅰ)求比賽4局乙勝的概率;
(Ⅱ)求在2局比賽中甲的勝局數為ξ的分布列和數學期望;
(Ⅲ)若規定贏一局得2分,平一局得1分,輸一局得0分,比賽進行五局,積分有超過5分者比賽結束,否則繼續進行,求甲得7分的概率.
(I)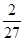 ;
;
(II) 分布列為: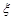
0 1 2 P 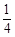
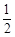
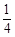
數學期望為1;
(Ⅲ)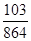
解析試題分析:(I)4局乙勝,即4局中乙3勝,且第4局為勝,前3局賽果為乙勝2局平1局或乙勝2局甲勝1局,所求概率為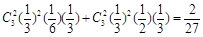 ,(II)甲的勝局數為ξ可取0,1,2,ξ取0包括輸2局或平兩局或1局輸1局平,所以
,(II)甲的勝局數為ξ可取0,1,2,ξ取0包括輸2局或平兩局或1局輸1局平,所以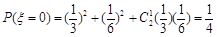 ,ξ取1包括1贏1輸或1贏1平,所以
,ξ取1包括1贏1輸或1贏1平,所以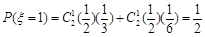 ,ξ取2包括2次都贏,所以
,ξ取2包括2次都贏,所以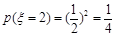 ,數學期望
,數學期望 ;(Ⅲ)甲若得7分, 要進行4局或5局比賽,且最后一局甲贏, 設比賽進行4局為事件A即為前3局要平1勝2,第4局勝,比賽進行5局為事件B即為前4局勝1平3或輸1平1勝2,第5局勝,則
;(Ⅲ)甲若得7分, 要進行4局或5局比賽,且最后一局甲贏, 設比賽進行4局為事件A即為前3局要平1勝2,第4局勝,比賽進行5局為事件B即為前4局勝1平3或輸1平1勝2,第5局勝,則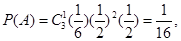
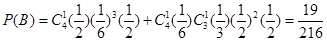 ,所以
,所以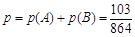 .
.
試題解析:由已知得甲贏的概率為 ,平的概率為
,平的概率為 ,輸的概率為
,輸的概率為 ,
,
乙贏的概率為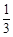 ,平的概率為
,平的概率為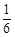 ,輸的概率為
,輸的概率為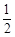 ,
,
(I)4局乙勝,即4局中乙3勝,且第4局為勝
所求的概率為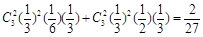
(II) 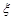 取0,1,2
取0,1,2 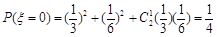
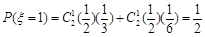
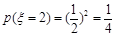
分布列如下: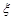
0 1 2 P 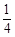
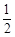
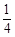

(Ⅲ)甲若得7分, 要進行4局或5局比賽,且最后一局甲贏, 設比賽進行4局事件為A,比賽進行5局事件為B,則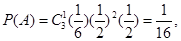
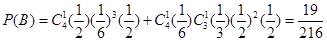 ,
,
所以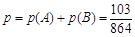
考點:概率分布列和數學期望


科目:高中數學 來源: 題型:解答題
一紙箱中放有除顏色外,其余完全相同的黑球和白球,其中黑球2個,白球3個.
(Ⅰ)從中同時摸出兩個球,求兩球顏色恰好相同的概率;
(Ⅱ)從中摸出一個球,放回后再摸出一個球,求兩球顏色恰好不同的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
甲乙兩班進行消防安全知識競賽,每班出3人組成甲乙兩支代表隊,首輪比賽每人一道必答題,答對則為本隊得1分,答錯不答都得0分,已知甲隊3人每人答對的概率分別為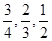 ,乙隊每人答對的概率都是
,乙隊每人答對的概率都是 .設每人回答正確與否相互之間沒有影響,用
.設每人回答正確與否相互之間沒有影響,用 表示甲隊總得分.
表示甲隊總得分.
(I)求隨機變量 的分布列及其數學期望E
的分布列及其數學期望E ;
;
(Ⅱ)求在甲隊和乙隊得分之和為4的條件下,甲隊比乙隊得分高的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
甲、乙兩人參加某電視臺舉辦的答題闖關游戲,按照規則,甲先從6道備選題中一次任意抽取3道題,獨立作答,然后由乙回答剩余3題,每人答對其中的2題就停止答題,即闖關成功。已知6道備選題中,甲能答對其中的4道題,乙答對每道題的概率都是 .
.
(1)求甲、乙至少有一人闖關成功的概率;
(2)設甲答對題目的個數為 ,求
,求 的分布列及數學期望.
的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
現有編號分別為1,2,3,4,5,6,7, 8,9的九道不同的數學題。某同學從這九道題中一次隨機抽取兩道題,每題被抽到的概率是相等的,用符號 表示事件“抽到兩 題的編號分別為
表示事件“抽到兩 題的編號分別為 ,且
,且 <
< ”.
”.
(1)共有多少個基本事件?并列舉出來;
(2)求該同學所抽取的兩道題的編號之和小于17但不小于11的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
一只不透明的袋子中裝有1個白球和1個紅球,這些球除顏色外其余都相同,攪勻后從中任意摸出1個球,記錄下顏色后放回袋中并攪勻,再從中任意摸出1個球,則 兩次摸出的球顏色相同的概率是 ;
兩次摸出的球顏色相同的概率是 ;
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com