【題目】已知﹣3≤log 
x≤﹣ 
，求函數f（x）=log2 
log2 
的值域．
【答案】解：∵﹣3≤log 
x≤﹣ 
，∴ 
，
即 
．
∵f（x）=log2
log2
=（log2x﹣log22）（log2x﹣log24）=（log2x﹣1）（log2x﹣2）．
令t=log2x，則 
，
∴f（x）=g（t）=（t﹣1）（t﹣2）= 
．
∵ ，
∴f（x）max=g（3）=2， 
．
∴函數f（x）=log2 log2 的值域為[﹣ 
，2]
【解析】由已知求得log2x的范圍，把f（x）=log2 
log2 
轉化為關于log2x的二次函數，換元后利用配方法求得函數的值域．
【考點精析】掌握三角函數的最值是解答本題的根本，需要知道函數
，當
時，取得最小值為
；當
時，取得最大值為
，則
，
，
．
天天向上一本好卷系列答案
小學生10分鐘應用題系列答案科目：高中數學 來源： 題型：
【題目】已知R上的奇函數f（x）和偶函數g（x）滿足f（x）+g（x）=ax﹣a﹣x+2（a＞0，且a≠1），若g（2）=a，則f（2）的值為（
A.
B.2
C.
D.a2
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】《漢字聽寫大會》不斷創收視新高，為了避免“書寫危機”弘揚傳統文化，某市對全市10萬名市民進行了漢字聽寫測試，調查數據顯示市民的成績服從正態分布
．現從某社區居民中隨機抽取50名市民進行聽寫測試，發現被測試市民正確書寫漢字的個數全部在160到184之間，將測試結果按如下方式分成六組：第一組
，第二組
，…，第六組
，如圖是按上述分組方法得到的頻率分布直方圖．
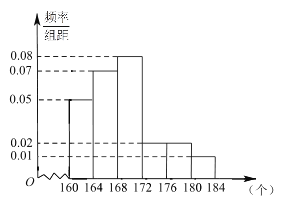
（1）試評估該社區被測試的50名市民的成績在全市市民中成績的平均狀況及這50名市民成績在172個以上（含172個）的人數；
（2）在這50名市民中成績在172個以上（含172個）的人中任意抽取2人，該2人中成績排名（從高到低）在全市前130名的人數記為
，求
的數學期望．
參考數據：若
～
，則
， 
， 
．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在四棱錐
中，AE⊥DE，CD⊥平面ADE，AB⊥平面ADE，CD=DA=6，AB=2，DE=3．
（1）求
到平面
的距離
（2）在線段
上是否存在一點
，使
？若存在，求出
的值；若不存在，說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在直角坐標系
中，已知中心在原點，離心率為
的橢圓
的一個焦點為圓
： 
的圓心．
（Ⅰ）求橢圓
的方程；
（Ⅱ）設
是橢圓
上一點，過
作兩條斜率之積為
的直線
， 
，當直線
， 
都與圓
相切時，求
的坐標．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）= 
+3lnax﹣x，g（x）=xex+cosx（a≠0）．
（1）求函數y=f（x）的單調區間；
（2）若x1∈[1，2]，x2∈[0，3]，使得f（ 
）＞g（x2）成立，求實數a的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】
年袁隆平的超級雜交水稻再創畝產量世界紀錄，為了測試水稻生長情況，專家選取了甲、乙兩塊地，從這兩塊地中隨機各抽取
株水稻樣本，測量他們的高度，獲得的高度數據的莖葉圖如圖所示：
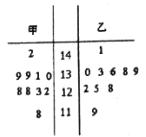
（1）根據莖葉圖判斷哪塊田的平均高度較高；
（2）計算甲乙兩塊地株高方差；
（3）現從乙地高度不低于
的樣本中隨機抽取兩株，求高度為
的樣本被抽中的概率.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】選修4-4：坐標系與參數方程
已知曲線
的極坐標方程為
，以極點為平面直角坐標系的原點，極軸為
的正半軸，建立平面直角坐標系
.
（1）若曲線
為參數）與曲線
相交于兩點
，求
；
（2）若
是曲線
上的動點，且點
的直角坐標為
，求
的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
