
【題目】如圖,在直三棱柱ABC﹣A1B1C1(側棱垂直于底面的棱柱)中,CA⊥CB,CA=CB=CC1=2,動點D在線段AB上.
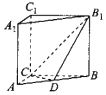
(1)求證:當點D為AB的中點時,平面B1CD⊥上平面ABB1A1;
(2)當AB=3AD時,求平面B1CD與平面BB1C1C所成的銳二面角的余弦值.
【答案】(1)見解析;(2)![]()
【解析】
(1)推導出![]() ,
,![]() ,
,![]() 平面
平面![]() ,由此能證明平面
,由此能證明平面![]() 上平面
上平面![]() .(2)
.(2)![]() ,
,![]() ,
,![]() 兩兩垂直,以
兩兩垂直,以![]() 為原點,
為原點,![]() ,
,![]() ,
,![]() 所在直線分別為
所在直線分別為![]() ,
,![]() ,
,![]() 軸,建立空間直角坐標系,利用向量法能求出平面
軸,建立空間直角坐標系,利用向量法能求出平面![]() 與平面
與平面![]() 所成的銳二面角的余弦值.
所成的銳二面角的余弦值.
(1)∵在等腰Rt△ABC中,D為斜邊AB的中點,∴CD⊥AB,
又∵在直三棱柱ABC﹣A1B1C1中,B1B⊥平面ABC,CD平面ABC,
∴B1B⊥CD,∵AB∩B1B=B,∴CD⊥平面ABB1A1,
又CD平面B1CD,∴平面B1CD⊥上平面ABB1A1.
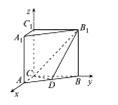
(2)如圖,∵CA,CB,CC1兩兩垂直,
∴以C為原點,CA,CB,CC1所在直線分別為x,y,z軸,建立空間直角坐標系,
則C(0,0,0),A(2,0,0),B(0,2,0),B1(0,2,2),D![]() ,
,
![]() (0,2,2),
(0,2,2),![]() ,
,
設平面B1CD的法向量![]() =(x,y,z),則
=(x,y,z),則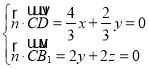 ,令z=1,得
,令z=1,得![]() ,
,
平面BB1C1C的法向量![]() =(2,0,0),
=(2,0,0),
設平面B1CD與平面BB1C1C所成的銳二面角的平面角為θ,
則cosθ=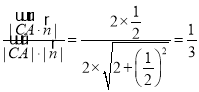 ,
,
∴平面B1CD與平面BB1C1C所成的銳二面角的余弦值為![]() .
.


 金牌教輔培優優選卷期末沖刺100分系列答案
金牌教輔培優優選卷期末沖刺100分系列答案科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 過點
過點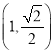 ,
,![]() 是該橢圓的左、右焦點,
是該橢圓的左、右焦點,![]() 是上頂點,且
是上頂點,且![]() 是等腰直角三角形.
是等腰直角三角形.
(1)求![]() 的方程;
的方程;
(2)已知![]() 是坐標原點,直線
是坐標原點,直線![]() 與橢圓
與橢圓![]() 相交于
相交于![]() 兩點,點
兩點,點![]() 在
在![]() 上且滿足四邊形
上且滿足四邊形![]() 是一個平行四邊形,求
是一個平行四邊形,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知在平面直角坐標系xOy中,橢圓C:![]() (a>b>0)離心率為
(a>b>0)離心率為![]() ,其短軸長為2.
,其短軸長為2.
(1)求橢圓C的標準方程;
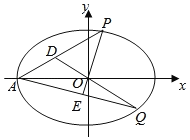
(2)如圖,A為橢圓C的左頂點,P,Q為橢圓C上兩動點,直線PO交AQ于E,直線QO交AP于D,直線OP與直線OQ的斜率分別為k1,k2,且k1k2=![]() ,
,![]()
![]() (λ,μ為非零實數),求λ2+μ2的值.
(λ,μ為非零實數),求λ2+μ2的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
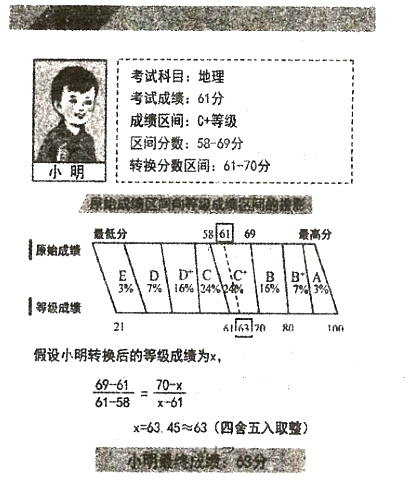
【題目】《山東省高考改革試點方案》規定:從![]() 年高考開始,高考物理、化學等六門選考科目的考生原始成績從高到低劃分為
年高考開始,高考物理、化學等六門選考科目的考生原始成績從高到低劃分為![]() 八個等級.參照正態分布原則,確定各等級人數所占比例分別為
八個等級.參照正態分布原則,確定各等級人數所占比例分別為![]() .選考科目成績計入考生總成績時,將
.選考科目成績計入考生總成績時,將![]() 至
至![]() 等級內的考生原始成績,依照等比例轉換法則分別轉換到
等級內的考生原始成績,依照等比例轉換法則分別轉換到![]()
![]() 八個分數區間,得到考生的等級成績.
八個分數區間,得到考生的等級成績.
某校![]() 級學生共
級學生共![]() 人,以期末考試成績為原始成績轉換了本校的等級成績,為學生合理選科提供依據,其中物理成績獲得等級
人,以期末考試成績為原始成績轉換了本校的等級成績,為學生合理選科提供依據,其中物理成績獲得等級![]() 的學生原始成績統計如下
的學生原始成績統計如下
成績 | 93 | 91 | 90 | 88 | 87 | 86 | 85 | 84 | 83 | 82 |
人數 | 1 | 1 | 4 | 2 | 4 | 3 | 3 | 3 | 2 | 7 |
(1)從物理成績獲得等級![]() 的學生中任取
的學生中任取![]() 名,求恰好有
名,求恰好有![]() 名同學的等級分數不小于
名同學的等級分數不小于![]() 的概率;
的概率;
(2)待到本級學生高考結束后,從全省考生中不放回的隨機抽取學生,直到抽到![]() 名同學的物理高考成績等級為
名同學的物理高考成績等級為![]() 或
或![]() 結束(最多抽取
結束(最多抽取![]() 人),設抽取的學生個數為
人),設抽取的學生個數為![]() ,求隨機變量
,求隨機變量![]() 的數學期望(注:
的數學期望(注: ![]() ).
).
查看答案和解析>>
科目:高中數學 來源: 題型:
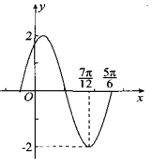
【題目】如圖是函數![]() 的部分圖象,將函數f(x)的圖象向右平移
的部分圖象,將函數f(x)的圖象向右平移![]() 個單位長度得到g(x)的圖象,給出下列四個命題:
個單位長度得到g(x)的圖象,給出下列四個命題:
①函數f(x)的表達式為![]() ;
;
②g(x)的一條對稱軸的方程可以為![]() ;
;
③對于實數m,恒有![]() ;
;
④f(x)+g(x)的最大值為2.其中正確的個數有( )
A. 1個B. 2個C. 3個D. 4個
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】眾所周知的“太極圖”,其形狀如對稱的陰陽兩魚互抱在一起,因而也被稱為“陰陽魚太極圖”.如圖是放在平面直角坐標系中的“太極圖”,整個圖形是一個圓形,其中黑色陰影區域在![]() 軸右側部分的邊界為一個半圓.給出以下命題:①在太極圖中隨機取一點,此點取自黑色陰影部分的概率是
軸右側部分的邊界為一個半圓.給出以下命題:①在太極圖中隨機取一點,此點取自黑色陰影部分的概率是![]() ;②當
;②當![]() 時,直線
時,直線![]() 與黑色陰影部分有公共點;③當
與黑色陰影部分有公共點;③當![]() 時,直線
時,直線![]() 與黑色陰影部分有兩個公共點.其中所有正確結論的序號是( )
與黑色陰影部分有兩個公共點.其中所有正確結論的序號是( )
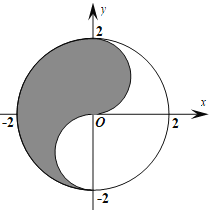
A.①B.①②C.①③D.①②③
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】[選修4-5:不等式選講]
已知函數f(x)=|2x﹣1|+|x+1|,g(x)=|x﹣a|+|x+a|.
(Ⅰ)解不等式f(x)>9;
(Ⅱ)x1∈R,x2∈R,使得f(x1)=g(x2),求實數a的取值范圍。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=Asin(ωx+![]() )(A>0,ω>0,|
)(A>0,ω>0,|![]() |<
|<![]() )的部分圖象如圖所示.
)的部分圖象如圖所示.
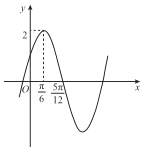
(Ⅰ)求f(x)的解析式;
(Ⅱ)若對于任意的x∈[0,m],f(x)≥1恒成立,求m的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 為矩形,平面
為矩形,平面![]()
![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 為
為![]() 中點.
中點.

(Ⅰ)求證:![]() ∥平面
∥平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)在棱![]() 上是否存在點
上是否存在點![]() ,使得
,使得![]()
![]() ?若存在,求
?若存在,求![]() 的值;若不存在,說明理由.
的值;若不存在,說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com