
【題目】[選修4-5:不等式選講]
已知函數f(x)=|2x﹣1|+|x+1|,g(x)=|x﹣a|+|x+a|.
(Ⅰ)解不等式f(x)>9;
(Ⅱ)x1∈R,x2∈R,使得f(x1)=g(x2),求實數a的取值范圍。
【答案】(1)![]() (2)
(2)![]()
【解析】試題分析:(1)絕對值函數分段討論解不等式。(2)由題意可得函數f(x)的值域是函數g(x)值域的子集,所以先求得f(x)的值域,再由絕對值不等式求得g(x)值域。
試題解析:(Ⅰ)不等式f(x)>9![]() ,或
,或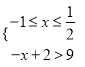 ,或
,或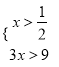 ,
,
即x<﹣3或∈或x>3,∴原不等式解集為(3,+∞)∪(﹣∞,3);
(Ⅱ)x1∈R,x2∈R,使得f(x1)=g(x2)函數f(x)的值域是函數g(x)值域的子集, 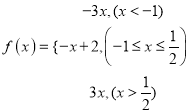 ,當x<﹣1時,﹣3x>3;
,當x<﹣1時,﹣3x>3;
當﹣1≤x![]() 時,
時, ![]() ﹣x+2≤3;當
﹣x+2≤3;當![]() 時,
時, ![]() ,
,
∴函數f(x)的值域是![]() ,g(x)=|x﹣a|+|x+a|≥|2a|,
,g(x)=|x﹣a|+|x+a|≥|2a|,
∴![]() ,即
,即![]() .∴實數a的取值范圍為[﹣
.∴實數a的取值范圍為[﹣![]() ,
, ![]() ].
].


科目:高中數學 來源: 題型:
【題目】某工廠有25周歲以上(含25周歲)工人300名,25周歲以 下工人200名.為研究工人的日平均生產量是否與年齡有關.現采用分層抽樣的方法,從中抽取了100名工人,先統計了他們某月的日平均生產件數,然后按工人年齡在“ 25周歲以上(含25周歲)”和“25周歲以下”分為兩組,再將兩組工人的日平均生產件數分成5組: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分別加以統計,得到如圖所示的頻率分布直方圖.
分別加以統計,得到如圖所示的頻率分布直方圖.

附表:
P( | 0.100 | 0 .010 | 0.001 |
k | 2.706 | 6.635 | 10.828 |
![]() ,(其中
,(其中 ![]() )
)
(1)從樣本中日平均生產件數不足60件的工人中隨機抽取2人,求至少抽到一名“25周歲以下組”工人的頻率.
(2)規定日平均生產件數不少于80件者為“生產能手”,請你根據已知條件完成 ![]() 的列聯表,并判斷是否有
的列聯表,并判斷是否有 ![]() 的把握認為“生產能手與工人所在的年齡組有關”?
的把握認為“生產能手與工人所在的年齡組有關”?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】[選修4-4:坐標系與參數方程]
已知直線l的參數方程為 (t為參數),曲線C的參數方程為
(t為參數),曲線C的參數方程為 (θ為參數),以坐標原點為極點,x軸的正半軸為極軸建立極坐標系,點P的極坐標為
(θ為參數),以坐標原點為極點,x軸的正半軸為極軸建立極坐標系,點P的極坐標為![]() 。
。
(Ⅰ)求直線l以及曲線C的極坐標方程;
(Ⅱ)設直線l與曲線C交于A,B兩點,求△PAB的面積。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】有下列說法: ①線性回歸分析就是由樣本點去尋找一條直線,使之貼近這些樣本點的數學方法;②利用樣本點的散點圖可以直觀判斷兩個變量的關系是否可以用線性關系表示;③通過回歸方程 ![]() ,可以估計和觀測變量的取值和變化趨勢;④因為由任何一組觀測值都可以求得一個線性回歸方程,所以沒有必要進行相關性檢驗.其中正確命題的個數是( )
,可以估計和觀測變量的取值和變化趨勢;④因為由任何一組觀測值都可以求得一個線性回歸方程,所以沒有必要進行相關性檢驗.其中正確命題的個數是( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列四個結論,其中正確的個數為( ). ①已 ![]() ,則
,則 ![]()
②過原點作曲線 ![]() 的切線,則切線方程為
的切線,則切線方程為 ![]() (其中e為自然對數的底數);
(其中e為自然對數的底數);
③已知隨機變 ![]()
![]() ,則
,則 ![]()
④已知n為正偶數,用數學歸納法證明等式 ![]() 時,若假設
時,若假設 ![]() 時,命題為真,則還需利用歸納假設再證明
時,命題為真,則還需利用歸納假設再證明 ![]() 時等式成立,即可證明等式對一切正偶數n都成立.
時等式成立,即可證明等式對一切正偶數n都成立.
⑤在回歸分析中,常用 ![]() 來刻畫回歸效果,在線性回歸模型中,
來刻畫回歸效果,在線性回歸模型中, ![]() 表示解釋變量對于預報變量變化的貢獻率
表示解釋變量對于預報變量變化的貢獻率 ![]() 越接近1,表示回歸的效果越好.
越接近1,表示回歸的效果越好.
A.2
B.3
C.4
D.5
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,直線AB經過☉O上的點C,并且OA=OB,CA=CB,☉O交直線OB于E,D兩點,連接EC,CD. 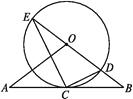
(1)求證:直線AB是☉O的切線;
(2)若tan∠CED= ![]() ,☉O的半徑為3,求OA的長.
,☉O的半徑為3,求OA的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com