
【題目】定義在R上的奇函數(shù)f(x),當x≥0時,f(x)= ![]() ,則關于x的函數(shù)F(x)=f(x)﹣a(0<a<1)的所有零點之和為( )
,則關于x的函數(shù)F(x)=f(x)﹣a(0<a<1)的所有零點之和為( )
A.3a﹣1
B.1﹣3a
C.3﹣a﹣1
D.1﹣3﹣a
【答案】B
【解析】解:∵定義在R上的奇函數(shù)f(x), ∴f(﹣x)=﹣f(x),
∵當x≥0時,f(x)= ![]() ,
,
∴當x≥0時,f(x)= 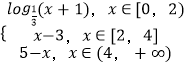 ,
,
得出x<0時,f(x)= ![]()
畫出圖象得出: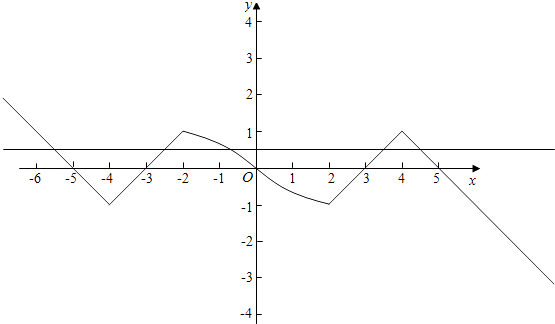
如圖從左向右零點為x1 , x2 , x3 , x4 , x5 ,
根據對稱性得出:x1+x2=﹣4×2=﹣8,
x4+x5=2×4=8,﹣log ![]() (﹣x3+1)=a,x3=1﹣3a ,
(﹣x3+1)=a,x3=1﹣3a ,
故x1+x2+x3+x4+x5=﹣8+1﹣3a+8=1﹣3a ,
故選:B
【考點精析】掌握函數(shù)的零點與方程根的關系是解答本題的根本,需要知道二次函數(shù)的零點:(1)△>0,方程 有兩不等實根,二次函數(shù)的圖象與 軸有兩個交點,二次函數(shù)有兩個零點;(2)△=0,方程 有兩相等實根(二重根),二次函數(shù)的圖象與 軸有一個交點,二次函數(shù)有一個二重零點或二階零點;(3)△<0,方程 無實根,二次函數(shù)的圖象與 軸無交點,二次函數(shù)無零點.


 云南師大附小一線名師提優(yōu)作業(yè)系列答案
云南師大附小一線名師提優(yōu)作業(yè)系列答案科目:高中數(shù)學 來源: 題型:
【題目】在平面直角坐標系xOy中,圓C的方程為x2+y2-8x+15=0,若直線y=kx-2上至少存在一點,使得以該點為圓心,1為半徑的圓與圓C有公共點,則k的最大值是____________.
【答案】![]()
【解析】∵圓C的方程可化為(x-4)2+y2=1,∴圓C的圓心為(4,0),半徑為1.由題意知,直線y=kx-2上至少存在一點A(x0,kx0-2),以該點為圓心,1為半徑的圓與圓C有公共點,∴存在x0∈R,使得AC≤1+1成立,即ACmin≤2.
∵ACmin即為點C到直線y=kx-2的距離![]() ,
,
∴![]() ≤2,解得0≤k≤
≤2,解得0≤k≤![]() .∴k的最大值是
.∴k的最大值是![]() .
.
【題型】填空題
【結束】
15
【題目】在平面直角坐標系![]() 中,直線
中,直線![]() .
.
(1)若直線![]() 與直線
與直線![]() 平行,求實數(shù)
平行,求實數(shù)![]() 的值;
的值;
(2)若![]() ,
, ![]() ,點
,點![]() 在直線
在直線![]() 上,已知
上,已知![]() 的中點在
的中點在![]() 軸上,求點
軸上,求點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】研究函數(shù)f(x)= ![]() 的性質,完成下面兩個問題:
的性質,完成下面兩個問題:
①將f(2),f(3),f(5)按從小到大排列為;
②函數(shù)g(x)= ![]() (x> 0)的最大值為 .
(x> 0)的最大值為 .
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
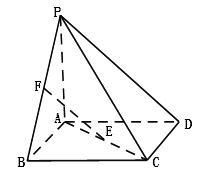
【題目】如圖,四棱錐 ![]() 的底面
的底面 ![]() 為正方形,
為正方形, ![]() ⊥底面
⊥底面 ![]() ,
, ![]() 分別是
分別是 ![]() 的中點,
的中點, ![]() .
.
(Ⅰ)求證 ![]() ∥平面
∥平面 ![]() ;
;
(Ⅱ)求直線 ![]() 與平面
與平面 ![]() 所成的角;
所成的角;
(Ⅲ)求四棱錐 ![]() 的外接球的體積.
的外接球的體積.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖所示的多面體中, ![]() 菱形,
菱形, ![]() 是矩形,
是矩形, ![]() ⊥平面
⊥平面 ![]() ,
, ![]() ,
, ![]() .
.
(Ⅰ)異面直線 ![]() 與
與 ![]() 所成的角余弦值;
所成的角余弦值;
(Ⅱ)求證平面 ![]() ⊥平面
⊥平面 ![]() ;
;
(Ⅲ)在線段 ![]() 取一點
取一點 ![]() ,當二面角
,當二面角 ![]() 的大小為60°時,求
的大小為60°時,求 ![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某化工廠擬建一個下部為圓柱,上部為半球的容器(如圖圓柱高為 ![]() ,半徑為
,半徑為 ![]() ,不計厚度,單位:米),按計劃容積為
,不計厚度,單位:米),按計劃容積為 ![]() 立方米,且
立方米,且 ![]() ,假設建造費用僅與表面積有關(圓柱底部不計 ),已知圓柱部分每平方米的費用為2千元,半球部分每平方米的費用為2千元,設該容器的建造費用為y千元.
,假設建造費用僅與表面積有關(圓柱底部不計 ),已知圓柱部分每平方米的費用為2千元,半球部分每平方米的費用為2千元,設該容器的建造費用為y千元.
(1)求y關于r的函數(shù)關系,并求其定義域;
(2)求建造費用最小時的 ![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】若![]() 的部分圖象如圖所示.
的部分圖象如圖所示.
(1)求函數(shù)![]() 的解析式;
的解析式;
(2)將![]() 的圖象向左平移
的圖象向左平移![]() 個單位長度得到
個單位長度得到![]() 的圖象,若
的圖象,若![]() 圖象的一個對稱軸為
圖象的一個對稱軸為![]() ,求
,求![]() 的最小值;
的最小值;
(3)在第(2)問的前提下,求函數(shù)![]() 在
在![]() 上的單調區(qū)間.
上的單調區(qū)間.

查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】《九章算術》中,將底面為長方形且有一條側棱與底面垂直的四棱錐稱之為陽馬,將四個面都為直角三角形的四面體稱之為鱉臑.如圖,在陽馬P﹣ABCD中,側棱PD⊥底面ABCD,且PD=CD,過棱PC的中點E,作EF⊥PB交PB于點F,連接DE,DF,BD,BE. 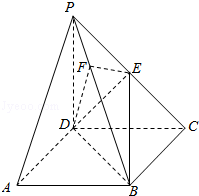
(1)證明:PB⊥平面DEF.試判斷四面體DBEF是否為鱉臑,若是,寫出其每個面的直角(只需寫出結論);若不是,說明理由;
(2)若面DEF與面ABCD所成二面角的大小為 ![]() ,求
,求 ![]() 的值.
的值.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com