
【題目】已知函數f(x)=|x﹣1|+|x+a|, ![]()
(1)當a=﹣2時,求不等式f(x)<g(x)的解集;
(2)若a>﹣1,且當x∈[﹣a,1]時,不等式f(x)≤g(x)有解,求實數a的取值范圍.
【答案】
(1)解:當a=﹣2時,
f(x)=|x﹣1|+|x﹣2|= 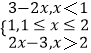 ,
,
∴f(x)<g(x)等價于 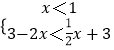 或
或 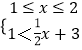 或
或  ,
,
解得0<x<1或1≤x≤2或2<x<4,即0<x<4.
∴不等式f(x)<g(x)的解集為{x|0<x<4}
(2)解:∵x∈[﹣a,1],∴f(x)=1﹣x+x+a=a+1,
不等式f(x)=a+1≤g(x)max=( ![]() )max,
)max,
∴﹣1<a≤ ![]() ,
,
∴實數a的取值范圍是(﹣1, ![]() ]
]
【解析】(1)當a=﹣2時,f(x)<g(x)等價于 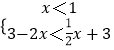 或
或 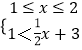 或
或 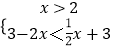 ,由此能求出不等式f(x)<g(x)的解集.(2)推導出f(x)=a+1,不等式f(x)≤a+1≤(
,由此能求出不等式f(x)<g(x)的解集.(2)推導出f(x)=a+1,不等式f(x)≤a+1≤( ![]() )max , 由此能求出實數a的取值范圍.
)max , 由此能求出實數a的取值范圍.


科目:高中數學 來源: 題型:
【題目】某企業生產一種產品,根據經驗,其次品率![]() 與日產量
與日產量![]() (萬件)之間滿足關系,
(萬件)之間滿足關系, (其中
(其中![]() 為常數,且
為常數,且![]() ,已知每生產1萬件合格的產品以盈利2萬元,但每生產1萬件次品將虧損1萬元(注:次品率=次品數/生產量, 如
,已知每生產1萬件合格的產品以盈利2萬元,但每生產1萬件次品將虧損1萬元(注:次品率=次品數/生產量, 如![]() 表示每生產10件產品,有1件次品,其余為合格品).
表示每生產10件產品,有1件次品,其余為合格品).
(1)試將生產這種產品每天的盈利額![]() (萬元)表示為日產量
(萬元)表示為日產量![]() (萬件)的函數;
(萬件)的函數;
(2)當日產量為多少時,可獲得最大利潤?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線C1:x2=2py(p>0),點A(p, ![]() )到拋物線C1的準線的距離為2.
)到拋物線C1的準線的距離為2.
(1)求拋物線C1的方程;
(2)過點A作圓C2:x2+(y﹣a)2=1的兩條切線,分別交拋物線于M,N兩點,若直線MN的斜率為﹣1,求實數a的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校團委會組織某班以小組為單位利用周末時間進行一次社會實踐活動,每個小組有5名同學,在活動結束后,學校團委會對該班的所有同學進行了測試,該班的A,B兩個小組所有同學得分(百分制)的莖葉圖如圖所示,其中B組一同學的分數已被污損,但知道B組學生的平均分比A組同學的平均分高一分.
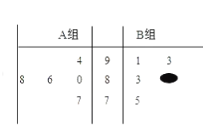
(1)若在B組學生中隨機挑選1人,求其得分超過86分的概率;
(2)現從A、B兩組學生中分別隨機抽取1名同學,設其分數分別為m、n,求![]() 的概率.
的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙兩人各射擊一次,擊中目標的概率分別是![]() 和
和![]() .假設兩人射擊是否擊中目標,相互之間沒有影響;每次射擊是否擊中目標,相互之間沒有影響.
.假設兩人射擊是否擊中目標,相互之間沒有影響;每次射擊是否擊中目標,相互之間沒有影響.
(1)求甲射擊4次,至少1次未擊中目標的概率;
(2)求兩人各射擊4次,甲恰好擊中目標2次且乙恰好擊中目標3次的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知變量![]() 之間的線性回歸方程為
之間的線性回歸方程為![]() ,且變量
,且變量![]() 之間的一組相關數據如表所示,則下列說法錯誤的是( )
之間的一組相關數據如表所示,則下列說法錯誤的是( )
x | 6 | 8 | 10 | 12 |
y | 6 | m | 3 | 2 |
A. 變量![]() 之間呈現負相關關系
之間呈現負相關關系
B. ![]() 的值等于5
的值等于5
C. 變量![]() 之間的相關系數
之間的相關系數![]()
D. 由表格數據知,該回歸直線必過點(9,4)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了鼓勵市民節約用電,實行“階梯式”電價,某邊遠山區每戶居民月用電量劃分為三檔:月用電量不超過150度,按0.6元/度收費,超過150度但不超過250度的部分每度加價0.1元,超過250度的部分每度再加價0.3元收費.
(1)求該邊遠山區某戶居民月用電費用![]() (單位:元)關于月用電量
(單位:元)關于月用電量![]() (單位:度)的函數解析式;
(單位:度)的函數解析式;
(2)已知該邊遠山區貧困戶的月用電量![]() (單位:度)與該戶長期居住的人口數
(單位:度)與該戶長期居住的人口數![]() (單位:人)間近似地滿足線性相關關系:
(單位:人)間近似地滿足線性相關關系:![]() (
(![]() 的值精確到整數),其數據如表:
的值精確到整數),其數據如表:
| 14 | 15 | 17 | 18 |
| 161 | 168 | 191 | 200 |
現政府為減輕貧困家庭的經濟負擔,計劃對該邊遠山區的貧困家庭進行一定的經濟補償,給出兩種補償方案供選擇:一是根據該家庭人數,每人每戶月補償6元;二是根據用電量每人每月補償![]() (
(![]() 為用電量)元,請根據家庭人數
為用電量)元,請根據家庭人數![]() 分析,一個貧困家庭選擇哪種補償方式可以獲得更多的補償?
分析,一個貧困家庭選擇哪種補償方式可以獲得更多的補償?
附:回歸直線![]() 中斜率和截距的最小二乘法估計公式分別為:
中斜率和截距的最小二乘法估計公式分別為:
 ,
,![]() .
.
參考數據:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,將從點M出發沿縱、橫方向到達點N的任一路徑稱為M到N的一條“L路徑”.如圖所示的路徑MM1M2M3N與路徑MN1N都是M到N的“L路徑”.某地有三個新建居民區,分別位于平面xOy內三點A(3,20),B(﹣10,0),C(14,0)處.現計劃在x軸上方區域(包含x軸)內的某一點P處修建一個文化中心.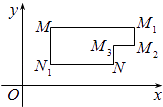
(1)寫出點P到居民區A的“L路徑”長度最小值的表達式(不要求證明);
(2)若以原點O為圓心,半徑為1的圓的內部是保護區,“L路徑”不能進入保護區,請確定點P的位置,使其到三個居民區的“L路徑”長度之和最小.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com