
【題目】如圖,正三棱柱![]() 的所有棱長均為2,
的所有棱長均為2, ![]() ,
, ![]() 分別為
分別為![]() 和
和![]() 的中點.
的中點.

(1)證明: ![]() 平面
平面![]() ;
;
(2)求點![]() 到平面
到平面![]() 的距離.
的距離.
【答案】(1)詳見解析;(2) ![]() .
.
【解析】試題分析:(1)證明線面垂直,一般方法為利用線面垂直的判定定理,即從線線垂直出發給予證明,而線線垂直的尋找與論證,可從兩個方面出發,一是利用面面垂直得線面垂直,再得線線垂直,二是利用平幾知識,如本題中正方形有關性質,(2)求點到直線距離,一般方法為利用等體積法,即根據![]() 可得
可得![]() 分別求出兩個三角形面積代入可得點
分別求出兩個三角形面積代入可得點![]() 到平面
到平面![]() 的距離.
的距離.
試題解析:(I)證明:由![]() 知
知![]() ,又平面
,又平面![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,而
,而![]()
![]() 平面
平面 ![]() ,∴
,∴![]() ,在正方形
,在正方形![]() 中,由
中,由![]() 分別是
分別是![]() 和
和![]() 的中點知
的中點知![]() ,而
,而![]() ,∴
,∴![]() 平面
平面![]() .
.
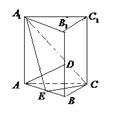
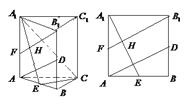
(Ⅱ)解法1: 由(I)![]() 平面
平面![]() ,過
,過![]() 點作
點作![]() , 交
, 交![]() 和
和![]() 分別于點
分別于點![]() 和
和![]() ,則
,則![]() 平面
平面![]() ,即
,即![]() 的長為
的長為![]() 到平面
到平面![]() 的距離, 在正方形
的距離, 在正方形![]() 中,易知
中,易知![]() ,
, ![]()
![]() ,即
,即![]() ,得
,得![]() ,故
,故![]() 到平面
到平面![]() 的距離為
的距離為![]() .
.
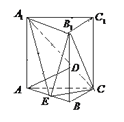
解法2:如圖,連接![]() ,在三棱錐
,在三棱錐![]() 中,設
中,設![]() 到平面
到平面![]() 的距離為
的距離為![]() ,則
,則![]() ,將
,將![]() ,
, ![]() 代入得
代入得![]() ,得
,得![]() , 故
, 故![]() 到平面
到平面![]() 的距離為
的距離為![]() .
.


科目:高中數學 來源: 題型:
【題目】在如圖所示的幾何體中,四邊形ABCD是菱形,ADNM是矩形,平面ADNM⊥平面ABCD,∠DAB=60°,AD=2,AM=1,E為AB的中點.
(Ⅰ)求證:AN∥平面MEC;
(Ⅱ)在線段AM上是否存在點P,使二面角P﹣EC﹣D的大小為![]() ?若存在,求出AP的長h;若不存在,請說明理由.
?若存在,求出AP的長h;若不存在,請說明理由.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設{an}是公比為正整數的等比數列,{bn}是等差數列,且a1a2a3=64,b1+b2+b3=﹣42,6a1+b1=2a3+b3=0.
(1)求數列{an}和{bn}的通項公式;
(2)設pn= ![]() ,數列{pn}的前n項和為Sn .
,數列{pn}的前n項和為Sn .
①試求最小的正整數n0 , 使得當n≥n0時,都有S2n>0成立;
②是否存在正整數m,n(m<n),使得Sm=Sn成立?若存在,請求出所有滿足條件的m,n;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某媒體為了解某地區大學生晚上放學后使用手機上網情況,隨機抽取了100名大學生進行調查.如圖是根據調查結果繪制的學生每晚使用手機上網平均所用時間的頻率分布直方圖.將時間不低于40分鐘的學生稱為“手機迷”. 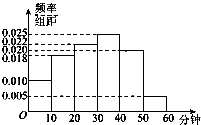
(1)樣本中“手機迷”有多少人?
(2)根據已知條件完成下面的2×2列聯表,并據此資料判斷是否有95%的把握認為“手機迷”與性別有關?
(3)將上述調查所得到的頻率視為概率.現在從該地區大量大學 生中,采用隨機抽樣方法每次抽取1名大學生,抽取3次,經調查一名“手機迷”比“非手機迷”每月的話費平均多40元,記被抽取的3名大學生中的“手機迷”人數為X,且設3人每月的總話費比“非手機迷”共多出Y元,若每次抽取的結果是相互獨立的,求X的分布列和Y的期望EY
查看答案和解析>>
科目:高中數學 來源: 題型:
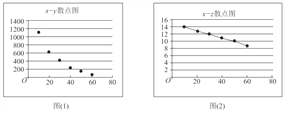
【題目】參加衡水中學數學選修課的同學,對某公司的一種產品銷量與價格進行統計,得到如下數據和散點圖:
定價 |
|
|
|
|
|
|
年銷售 |
|
|
|
|
|
|
|
|
|
|
|
|
|
(參考數據:![]()
![]() )
)
(I)根據散點圖判斷,![]() 與
與![]() ,
,![]() 與
與![]() 哪一對具有較強的線性相關性(給出判斷即可,不必說明理由)?
哪一對具有較強的線性相關性(給出判斷即可,不必說明理由)?
(II)根據(I)的判斷結果有數據,建立![]() 關于
關于![]() 的回歸方程(方程中的系數均保留兩位有效數字);
的回歸方程(方程中的系數均保留兩位有效數字);
(III)定價為多少元/![]() 時,年利潤的預報值最大?
時,年利潤的預報值最大?
附:對一組數據![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計分別為:
的斜率和截距的最小二乘估計分別為: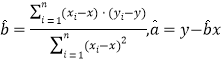 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設等差數列{an}的前n項和為Sn , a2=4,S5=30
(1)求數列{an}的通項公式an
(2)設數列{ ![]() }的前n項和為Tn , 求證:
}的前n項和為Tn , 求證: ![]() ≤Tn<
≤Tn< ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某搜索引擎廣告按照付費價格對搜索結果進行排名,點擊一次付費價格排名越靠前,被點擊的次數也可能會提高,已知某關鍵詞被甲、乙等多個公司競爭,其中甲、乙付費情況與每小時點擊量結果繪制成如下的折線圖.

(1)試根據所給數據計算每小時點擊次數的均值方差并分析兩組數據的特征;
(2)若把乙公司設置的每次點擊價格為x,每小時點擊次數為![]() ,則點
,則點![]() 近似在一條直線附近.試根據前5次價格與每小時點擊次數的關系,求y關于x的回歸直線
近似在一條直線附近.試根據前5次價格與每小時點擊次數的關系,求y關于x的回歸直線![]() .(附:回歸方程系數公式:
.(附:回歸方程系數公式: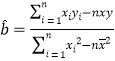 ,
,![]() ).
).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線 ![]() x+y﹣
x+y﹣ ![]() =0經過橢圓C:
=0經過橢圓C: ![]() +
+ ![]() =1(a>b>0)的右焦點和上頂點.
=1(a>b>0)的右焦點和上頂點.
(1)求橢圓C的標準方程;
(2)過點(0,﹣2)的直線l與橢圓C交于不同的A,B兩點,若∠AOB為鈍角,求直線l的斜率k的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com