
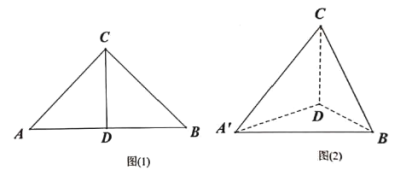
【題目】如圖(1)在等腰直角![]() 中,斜邊
中,斜邊![]() ,
,![]() 為
為![]() 的中點,將
的中點,將![]() 沿
沿![]() 折疊得到如圖(2)所示的三棱錐
折疊得到如圖(2)所示的三棱錐![]() .若三棱錐
.若三棱錐![]() 的外接球的半徑為3,則
的外接球的半徑為3,則![]() 的余弦值______.
的余弦值______.
科目:高中數學 來源: 題型:
【題目】已知非空集合![]() 是由一些函數組成,滿足如下性質:①對任意
是由一些函數組成,滿足如下性質:①對任意![]() ,
,![]() 均存在反函數
均存在反函數![]() ,且
,且![]() ;②對任意
;②對任意![]() ,方程
,方程![]() 均有解;③對任意
均有解;③對任意![]() 、
、![]() ,若函數
,若函數![]() 為定義在
為定義在![]() 上的一次函數,則
上的一次函數,則![]() .
.
(1)若![]() ,
,![]() ,均在集合
,均在集合![]() 中,求證:函數
中,求證:函數![]() ;
;
(2)若函數![]() (
(![]() )在集合
)在集合![]() 中,求實數
中,求實數![]() 的取值范圍;
的取值范圍;
(3)若集合![]() 中的函數均為定義在
中的函數均為定義在![]() 上的一次函數,求證:存在一個實數
上的一次函數,求證:存在一個實數![]() ,使得對一切
,使得對一切![]() ,均有
,均有![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在空間直角坐標系O-xyz中,已知正四棱錐PABCD的高OP=2,點B,D和C,A分別在x軸和y軸上,且AB=![]() ,點M是棱PC的中點.
,點M是棱PC的中點.
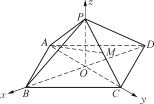
(1)求直線AM與平面PAB所成角的正弦值;
(2)求二面角A-PB-C的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若![]() 、
、![]() 兩點分別在函數
兩點分別在函數![]() 與
與![]() 的圖像上,且關于直線
的圖像上,且關于直線![]() 對稱,則稱
對稱,則稱![]() 、
、![]() 是
是![]() 與
與![]() 的一對“伴點”(
的一對“伴點”(![]() 、
、![]() 與
與![]() 、
、![]() 視為相同的一對).已知
視為相同的一對).已知 ,
,![]() ,若
,若![]() 與
與![]() 存在兩對“伴點”,則實數
存在兩對“伴點”,則實數![]() 的取值范圍為________.
的取值范圍為________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線C:![]() (
(![]() )的焦點F到準線l的距離為2,直線
)的焦點F到準線l的距離為2,直線![]() 過點F且與拋物線交于M、N兩點,直線
過點F且與拋物線交于M、N兩點,直線![]() 過坐標原點O及點M且與l交于點P,點Q在線段
過坐標原點O及點M且與l交于點P,點Q在線段![]() 上.
上.
(1)求直線![]() 的斜率;
的斜率;
(2)若![]() ,
,![]() ,
,![]() 成等差數列,求點Q的軌跡方程.
成等差數列,求點Q的軌跡方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】現有下列四個結論,其中所有正確結論的編號是___________.
①若![]() ,則
,則![]() 的最大值為
的最大值為![]() ;
;
②若![]() ,
,![]() ,
,![]() 是等差數列
是等差數列![]() 的前
的前![]() 項,則
項,則![]() ;
;
③“![]() ”的一個必要不充分條件是“
”的一個必要不充分條件是“![]() ”;
”;
④“![]() ,
,![]() ”的否定為“
”的否定為“![]() ,
,![]() ”.
”.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com