
【題目】已知函數![]() ,
,![]() .
.
(1)當![]() 時,總有
時,總有![]() ,求
,求![]() 的最小值;
的最小值;
(2)對于![]() 中任意
中任意![]() 恒有
恒有![]() ,求
,求![]() 的取值范圍.
的取值范圍.
 教材全解字詞句篇系列答案
教材全解字詞句篇系列答案科目:高中數學 來源: 題型:
【題目】已知數列{an}滿足:a1+a2+a3+…+an=n-an,(n=1,2,3,…)
(Ⅰ)求證:數列{an-1}是等比數列;
(Ⅱ)令bn=(2-n)(an-1)(n=1,2,3,…),如果對任意n∈N*,都有bn+![]() t≤t2,求實數t的取值范圍.
t≤t2,求實數t的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 在區間
在區間![]() 上有且僅有2個零點,對于下列4個結論:①在區間
上有且僅有2個零點,對于下列4個結論:①在區間![]() 上存在
上存在![]() ,滿足
,滿足![]() ;②
;②![]() 在區間
在區間![]() 有且僅有1個最大值點;③
有且僅有1個最大值點;③![]() 在區間
在區間![]() 上單調遞增;④
上單調遞增;④![]() 的取值范圍是
的取值范圍是![]() ,其中所有正確結論的編號是( )
,其中所有正確結論的編號是( )
A.①③B.①③④C.②③D.①④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數y=f(x),x∈[1,+∞),數列{an}滿足![]() ,
,
①函數f(x)是增函數;
②數列{an}是遞增數列.
寫出一個滿足①的函數f(x)的解析式______.
寫出一個滿足②但不滿足①的函數f(x)的解析式______.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】數列![]() :
: ![]() 滿足:
滿足: ![]() .記
.記![]() 的前
的前![]() 項和為
項和為![]() ,并規定
,并規定![]() .定義集合
.定義集合![]() ,
, ![]()
![]() ,
, ![]() .
.
(Ⅰ)對數列![]() :
: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,求集合
,求集合![]() ;
;
(Ⅱ)若集合![]() ,
, ![]() ,證明:
,證明: ![]() ;
;
(Ⅲ)給定正整數![]() .對所有滿足
.對所有滿足![]() 的數列
的數列![]() ,求集合
,求集合![]() 的元素個數的最小值.
的元素個數的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】明朝的程大位在《算法統宗》中(1592年),有這么個算法歌訣:三人同行七十稀,五樹梅花廿一枝,七子團圓正半月,除百零五便得知.它的意思是說:求某個數(正整數)的最小正整數值,可以將某數除以3所得的余數乘以70,除以5所得的余數乘以21,除以7所得的余數乘以15,再將所得的三個積相加,并逐次減去105,減到差小于105為止,所得結果就是這個數的最小正整數值.《孫子算經》上有一道極其有名的“物不知數”問題:“今有物不知其數,三三數之余二,五五數之余三,七七數之余二,問物幾何.”用上面的算法歌訣來算,該物品最少是幾件( )
A.21B.22C.23D.24
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】近年來,“無樁有站”模式的公共自行車日益普及,即傳統自行車加裝智能鎖,實現掃碼租車及刷卡租車、某公司量產了甲、乙兩種款式的公共自行車并投人使用,為了調查消費者對兩種自行車的租賃情況,現隨機抽取這兩種款式的自行車各100輛,分別統計了每輛車在某周內的出租次數,得到甲、乙兩種自行車這周內出租次數的頻數分布表:
甲 | |||||
出租次數(單位:次) |
|
|
|
|
|
頻數 | 10 | 10 | 60 | 15 | 5 |
乙 | |||||
出租次數(單位:次) |
|
|
|
|
|
頻數 | 20 | 25 | 25 | 10 | 20 |
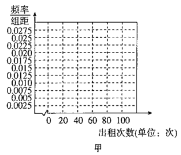
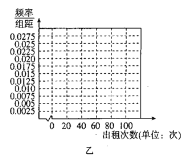
(1)根據頻數分布表,完成上面頻率分布直方圖,并根據頻率分布直方圖比較甲、乙兩種自行車這周內出租次數方差的大小(不必說明理由);
(2)如果兩種自行車每次出租獲得的利潤相同,該公司決定大批量生產其中一種投入某城市使用,請你根據所學的統計知識,給出建議應該生產哪一種自行車,并說明你的理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com