【題目】近一段時間來，由于受非洲豬瘟的影響，各地豬肉價格普遍上漲，生豬供不應求。各大養豬場正面臨巨大挑戰，目前各項針對性政策措施對于生豬整體產能恢復、激發養殖戶積極性的作用正在逐步顯現．
現有甲、乙兩個規模一致的大型養豬場，均養有1萬頭豬.根據豬的重量，將其分為三個成長階段如下表．
豬生長的三個階段
階段 | 幼年期 | 成長期 | 成年期 |
重量（Kg） |
|
|
|
根據以往經驗，兩個養豬場內豬的體重
均近似服從正態分布
.
由于我國有關部門加強對大型養豬場即將投放市場的成年期的豬監控力度，高度重視其質量保證，為了養出健康的成年活豬，甲、乙兩養豬場引入兩種不同的防控及養殖模式．已知甲、乙兩個養豬場內一頭成年期豬能通過質檢合格的概率分別為
，
．
（1）試估算各養豬場三個階段的豬的數量；
（2）已知甲養豬場出售一頭成年期的豬，若為健康合格的豬 ，則可盈利
元，若為不合格的豬，則虧損
元；乙養豬場出售一頭成年期的豬，若為健康合格的豬 ，則可盈利
元，若為不合格的豬，則虧損
元．記
為甲、乙養豬場各出售一頭成年期豬所得的總利潤，求隨機變量的分布列，假設兩養豬場均能把成年期豬售完，求兩養豬場的總利潤期望值．
（參考數據：若
，則
，
，
）
【答案】（1）甲、乙兩養豬場各有幼年期豬
頭，成長期豬
頭，成年期豬頭；（2）分布列見解析，135450元.
【解析】
（1）根據正態分布的相關知識進行計算即可；
（2）根據甲、乙兩個養豬場內一頭成年期豬能通過質檢合格的概率分別為
，
，隨機變量
可能取值為
，
，
，分別求出
，
，
，寫出分布列和期望即可.
（1）由于豬的體重
近似服從正態分布
，設各階段豬的數量分別為
∴
，
∴
（頭）；
同理，
，
∴
（頭）；
，
∴
（頭）.
所以，甲、乙兩養豬場各有幼年期豬頭，成長期豬頭，成年期豬頭。
（2）依題意，甲、乙兩個養豬場內一頭成年期豬能通過質檢合格的概率分別為，，隨機變量可能取值為，，.
，
，
，
所以的分布列為：
| | | |
| | | |
所以
（元），
由于各養豬場均有頭成年豬，一頭豬出售的利潤總和的期望為
元，則總利潤期望為
（元）.
陽光課堂課時優化作業系列答案科目：高中數學 來源： 題型：
【題目】已知函數f（x）＝2xlnx﹣x
2．
（1）求曲線y＝f（x）在點（1，f（1））處的切線方程
（2）若方程f′（x）＝a在[
，+∞）有且僅有兩個實根（其中f′（x）為f（x）的導函數，e為自然對數的底），求實數a的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在四棱錐P－ABCD中，底面ABCD為矩形，平面PAB⊥平面ABCD，AB＝AP＝3，AD＝PB＝2，E為線段AB上一點，且AE︰EB＝7︰2，點F、G分別為線段PA、PD的中點．
（1）求證：PE⊥平面ABCD；
（2）若平面EFG將四棱錐P－ABCD分成左右兩部分，求這兩部分的體積之比．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】[選修4-4：坐標系與參數方程]
在直角坐標系
中，曲線
的參數方程為
（
為參數），直線
的方程為
．
（1）以坐標原點為極點，
軸的正半軸為極軸建立極坐標系，求曲線的極坐標方程和直線的極坐標方程；
（2）在（1）的條件下，直線
的極坐標方程為
，設曲線與直線的交于點
和點
，曲線與直線的交于點和點
，求
的面積．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】我們把定義在
上，且滿足
（其中常數
，
滿足
，
，
）的函數叫做似周期函數.
（1）若某個似周期函數
滿足
且圖像關于直線
對稱，求證：函數
是偶函數；
（2）當，
時，某個似周期函數在
時的解析式為
，求函數，
的解析式；
（3）對于確定的
且當
時，
，試研究似周期函數在區間
上是否可能是單調函數？若可能，求出的取值范圍；若不可能，請說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）＝cos（2x
）+2sin（
）sin（
x）．
（Ⅰ）求f（x）的單調遞增區間；
（Ⅱ）求函數y＝f（x）的對稱軸方程，并求函數f（x）在區間[
，
]上的最大值和最小值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在四棱錐P–ABCD中，PA⊥平面ABCD，AD⊥CD，AD∥BC，PA=AD=CD=2，BC=3．E為PD的中點，點F在PC上，且
．
（Ⅰ）求證：CD⊥平面PAD；
（Ⅱ）求二面角F–AE–P的余弦值；
（Ⅲ）設點G在PB上，且
．判斷直線AG是否在平面AEF內，說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某商場為吸引顧客消費推出一項優惠活動．活動規則如下：消費額每滿100元可轉動如圖所示的轉盤一次，并獲得相應金額的返券，假定指針等可能地停在任一位置.若指針停在A區域返券60元；停在B區域返券30元；停在C區域不返券.例如：消費218元，可轉動轉盤2次，所獲得的返券金額是兩次金額之和．
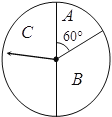
（1）若某位顧客消費128元，求返券金額不低于30元的概率；
（2）若某位顧客恰好消費280元，并按規則參與了活動，他獲得返券的金額記為
（元）．求隨機變量
的分布列和數學期望．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
