
【題目】已知函數f(x)=A cos(ωx+φ)(A>0,ω>0)的部分圖象如圖所示,下面結論錯誤的是( )

A. 函數f(x)的最小正周期為![]()
B. 函數f(x)的圖象可由g(x)=Acos ωx的圖象向右平移![]() 個單位長度得到
個單位長度得到
C. 函數f(x)的圖象關于直線x=![]() 對稱
對稱
D. 函數f(x)在區間![]() 上單調遞增
上單調遞增
【答案】D
【解析】∵由題意可知,此函數的周期T=2(![]() ﹣
﹣![]() )
)![]() ,
,
∴解得:ω=3,可得:f(x)=Acos(3x+φ).
又∵由題圖可知f(![]() )=Acos(3×
)=Acos(3×![]() +φ)=Acos(φ﹣
+φ)=Acos(φ﹣![]() π)=0,
π)=0,
∴利用五點作圖法可得:φ﹣![]() π=
π=![]() ,解得:φ=
,解得:φ=![]() ,
,
∴f(x)=Acos(3x+![]() ).
).
∴令3x+![]() =kπ,k∈Z,可解得函數的對稱軸方程為:x=
=kπ,k∈Z,可解得函數的對稱軸方程為:x=![]() ﹣
﹣![]() ,k∈Z,
,k∈Z,
令2kπ﹣π≤3x+![]() ≤2kπ,k∈Z,可解得:
≤2kπ,k∈Z,可解得: ![]() kπ﹣
kπ﹣![]() ≤x≤
≤x≤![]() kπ﹣
kπ﹣![]() ,k∈Z,
,k∈Z,
故函數的單調遞增區間為:[![]() kπ﹣
kπ﹣![]() ,
, ![]() kπ﹣
kπ﹣![]() ],k∈Z.
],k∈Z.
∴對于A,函數f(x)的最小周期為![]() ,故A正確;
,故A正確;
對于B,因為g(x)=Acos3x的圖象向右平移![]() 個單位得到y=Acos[3(x﹣
個單位得到y=Acos[3(x﹣![]() )]=Acos(3x﹣
)]=Acos(3x﹣![]() )=Acos(3x﹣
)=Acos(3x﹣![]() )=Acos(3x+
)=Acos(3x+![]() )=f(x),故B正確;
)=f(x),故B正確;
對于C,因為函數的對稱軸方程為:x=![]() ﹣
﹣![]() ,k∈Z,令k=2,可得函數f(x)的圖象關于直線x=
,k∈Z,令k=2,可得函數f(x)的圖象關于直線x=![]() 對稱,故C正確;
對稱,故C正確;
對于D,因為函數的單調遞增區間為:[![]() kπ﹣
kπ﹣![]() ,
, ![]() kπ﹣
kπ﹣![]() ],k∈Z,令k=2,可得函數單調遞增區間為:[
],k∈Z,令k=2,可得函數單調遞增區間為:[![]() ,
, ![]() ],故函數f(x)在區間(
],故函數f(x)在區間(![]() ,
, ![]() )上不單調遞增,故D錯誤.
)上不單調遞增,故D錯誤.
故選:D.


科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的中心在原點,其中一個焦點與拋物線
的中心在原點,其中一個焦點與拋物線![]() 的焦點重合,點
的焦點重合,點![]() 在橢圓
在橢圓![]() 上.
上.
(1)求橢圓![]() 的方程;
的方程;
(2)設橢圓的左右焦點分別為![]() ,過
,過![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 相交于
相交于![]() 兩點,若
兩點,若![]() 的面積為
的面積為![]() ,求以
,求以![]() 為圓心且與直線
為圓心且與直線![]() 相切的圓的方程.
相切的圓的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲乙兩地相距![]() 海里,某貨輪勻速行駛從甲地運輸貨物到乙地,運輸成本包括燃料費用和其他費用.已知該貨輪每小時的燃料費與其速度的平方成正比,比例系數為
海里,某貨輪勻速行駛從甲地運輸貨物到乙地,運輸成本包括燃料費用和其他費用.已知該貨輪每小時的燃料費與其速度的平方成正比,比例系數為![]() ,其他費用為每小時
,其他費用為每小時![]() 元,且該貨輪的最大航行速度為
元,且該貨輪的最大航行速度為![]() 海里/小時.
海里/小時.
(![]() )請將該貨輪從甲地到乙地的運輸成本
)請將該貨輪從甲地到乙地的運輸成本![]() 表示為航行速度
表示為航行速度![]() (海里/小時)的函數.
(海里/小時)的函數.
(![]() )要使從甲地到乙地的運輸成本最少,該貨輪應以多大的航行速度行駛?
)要使從甲地到乙地的運輸成本最少,該貨輪應以多大的航行速度行駛?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如果雙曲線的離心率e=![]() ,則稱此雙曲線為黃金雙曲線.有以下幾個命題:①雙曲線
,則稱此雙曲線為黃金雙曲線.有以下幾個命題:①雙曲線![]() 是黃金雙曲線;②雙曲線
是黃金雙曲線;②雙曲線![]() 是黃金雙曲線;③在雙曲線
是黃金雙曲線;③在雙曲線![]() (a>0,b>0)中,F1為左焦點,A2為右頂點,B1(0,b),若∠F1B1A2=90°,則該雙曲線是黃金雙曲線;④在雙曲線
(a>0,b>0)中,F1為左焦點,A2為右頂點,B1(0,b),若∠F1B1A2=90°,則該雙曲線是黃金雙曲線;④在雙曲線![]() (a>0,b>0)中,過右焦點F2作實軸的垂線交雙曲線于M,N兩點,O為坐標原點,若∠MON=120°,則該雙曲線是黃金雙曲線.其中正確命題的序號為________.
(a>0,b>0)中,過右焦點F2作實軸的垂線交雙曲線于M,N兩點,O為坐標原點,若∠MON=120°,則該雙曲線是黃金雙曲線.其中正確命題的序號為________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】將函數f(x)=sin 2x+![]() cos 2x圖象上所有點的橫坐標伸長到原來的2倍(縱坐標不變),再將圖象上所有點向右平移
cos 2x圖象上所有點的橫坐標伸長到原來的2倍(縱坐標不變),再將圖象上所有點向右平移![]() 個單位長度,得到函數g(x)的圖象,則g(x)圖象的一條對稱軸方程是( )
個單位長度,得到函數g(x)的圖象,則g(x)圖象的一條對稱軸方程是( )
A. x=-![]() B. x=
B. x=![]()
C. x=![]() D. x=
D. x=![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在直角坐標系中,曲線![]() :
: ![]() 經過伸縮變換
經過伸縮變換![]() 后得到曲線
后得到曲線![]() .以坐標原點
.以坐標原點![]() 為極點,
為極點, ![]() 軸的正半軸為極軸建立極坐標系,曲線
軸的正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(Ⅰ)求出曲線![]() 、
、![]() 的參數方程;
的參數方程;
(Ⅱ)若![]() 、
、![]() 分別是曲線
分別是曲線![]() 、
、![]() 上的動點,求
上的動點,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
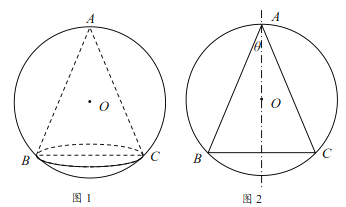
【題目】某藝術品公司欲生產一款迎新春工藝禮品,該禮品是由玻璃球面和該球的內接圓錐組成,圓錐的側面用于藝術裝飾,如圖1.為了便于設計,可將該禮品看成是由圓![]() 及其內接等腰三角形
及其內接等腰三角形![]() 繞底邊
繞底邊![]() 上的高所在直線
上的高所在直線![]() 旋轉180°而成,如圖2.已知圓
旋轉180°而成,如圖2.已知圓![]() 的半徑為
的半徑為![]() ,設
,設![]() ,圓錐的側面積為
,圓錐的側面積為![]() .
.
(1)求![]() 關于
關于![]() 的函數關系式;
的函數關系式;
(2)為了達到最佳觀賞效果,要求圓錐的側面積![]() 最大.求
最大.求![]() 取得最大值時腰
取得最大值時腰![]() 的長度.
的長度.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com