
【題目】一個(gè)正方體的平面展開圖及該正方體的直觀圖的示意圖如圖所示.在正方體中,設(shè)BC的中點(diǎn)為M,GH的中點(diǎn)為N.

(1)請(qǐng)將字母F,G,H標(biāo)記在正方體相應(yīng)的頂點(diǎn)處(不需說明理由).
(2)判斷平面BEG與平面ACH的位置關(guān)系,并證明你的結(jié)論.
【答案】(1) 見解析(2) 見解析
【解析】試題分析:(Ⅰ)直接標(biāo)出點(diǎn)F,G,H的位置.
(Ⅱ)先證BCHE為平行四邊形,可以知道BE∥平面ACH,同理可證BG∥平面ACH,即可證明平面BEG∥平面ACH.
試題解析:(1)點(diǎn)F,G,H的位置如圖所示.
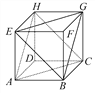
(2)平面BEG∥平面ACH.證明如下:
因?yàn)锳BCD-EFGH為正方體,
所以BC∥FG,BC=FG,
又FG∥EH,F(xiàn)G=EH,所以BC∥EH,BC=EH
于是BCHE為平行四邊形.所以BE∥CH,
又CH平面ACH,BE平面ACH,
所以BE∥平面ACH.同理BG∥平面ACH,
又BE∩BG=B,所以平面BEG∥平面ACH.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
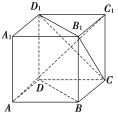
【題目】【2017唐山模擬】如圖,ABCDA1B1C1D1為正方體,連接BD,AC1,B1D1,CD1,B1C,現(xiàn)有以下幾個(gè)結(jié)論:①BD∥平面CB1D1;②AC1⊥平面CB1D1;③AC1與底面ABCD所成角的正切值是![]() ;④CB1與BD為異面直線,其中所有正確結(jié)論的序號(hào)為________.
;④CB1與BD為異面直線,其中所有正確結(jié)論的序號(hào)為________.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè) ![]() ,函數(shù)
,函數(shù) ![]()
(1)若 ![]() 在
在 ![]() 上單調(diào)遞增,求
上單調(diào)遞增,求 ![]() 的取值范圍;
的取值范圍;
(2)記 ![]() 為
為 ![]() 在
在 ![]() 上的最大值,求
上的最大值,求 ![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知△ABC的三個(gè)內(nèi)角A、B、C所對(duì)的邊分別是a、b、c,向量m=(cos B,cos C),n=(2a+c,b),且m⊥n.
(1)求角B的大小;
(2)若b=![]() ,求a+c的取值范圍.
,求a+c的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】過點(diǎn)P(1,2)引直線,使A(2,3),B(4,-5)到它的距離相等,則這條直線的方程為 ( )
A. 4x+y-6=0
B. x+4y-6=0
C. 2x+3y-7=0或x+4y-6=0
D. 3x+2y-7=0或4x+y-6=0
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)的圖像與函數(shù)h(x)=![]() 的圖像關(guān)于點(diǎn)A(0,1)對(duì)稱。
的圖像關(guān)于點(diǎn)A(0,1)對(duì)稱。
(1)求函數(shù)f(x)的解析式;
(2)若g(x)=xf(x)+ax,且g(x)在區(qū)間(0,4]上為減函數(shù),求實(shí)數(shù)a的取值范圍。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
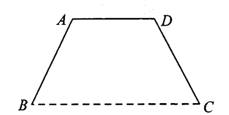
【題目】某單位將舉辦慶典活動(dòng),要在廣場(chǎng)上豎立一形狀為等腰梯形的彩門![]() (如圖).設(shè)計(jì)要求彩門的面積為
(如圖).設(shè)計(jì)要求彩門的面積為![]() (單位:
(單位:![]() ),高為
),高為![]() (單位:
(單位:![]() )(
)(![]() 為常數(shù)).彩門的下底
為常數(shù)).彩門的下底![]() 固定在廣場(chǎng)底面上,上底和兩腰由不銹鋼支架構(gòu)成,設(shè)腰和下底的夾角為
固定在廣場(chǎng)底面上,上底和兩腰由不銹鋼支架構(gòu)成,設(shè)腰和下底的夾角為![]() ,不銹鋼支架的長(zhǎng)度和記為
,不銹鋼支架的長(zhǎng)度和記為![]() .
.
(1)請(qǐng)將![]() 表示成關(guān)于
表示成關(guān)于![]() 的函數(shù)
的函數(shù)![]() ;
;
(2)問當(dāng)![]() 為何值
為何值![]() 最小,并求最小值.
最小,并求最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在正方體ABCD-A1B1C1D1中,M,N,Q分別是棱D1C1,A1D1,BC的中點(diǎn),P在對(duì)角線BD1上,且BP=![]() BD1,給出下面四個(gè)命題:
BD1,給出下面四個(gè)命題:
(1)MN∥平面APC;(2)C1Q∥平面APC;(3)A,P,M三點(diǎn)共線;(4)平面MNQ∥平面APC.正確的序號(hào)為 ( )
A. (1)(2) B. (1)(4) C. (2)(3) D. (3)(4)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知直角梯形![]() 中,
中,![]() 是邊長(zhǎng)為2的等邊三角形,
是邊長(zhǎng)為2的等邊三角形,![]() .沿
.沿![]() 將
將![]() 折起,使
折起,使![]() 至
至![]() 處,且
處,且![]() ;然后再將
;然后再將![]() 沿
沿![]() 折起,使
折起,使![]() 至
至![]() 處,且面
處,且面![]() 面
面![]() ,
,![]() 和
和![]() 在面
在面![]() 的同側(cè).
的同側(cè).

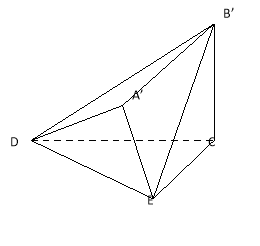
(Ⅰ) 求證:![]() 平面
平面![]() ;
;
(Ⅱ) 求平面![]() 與平面
與平面![]() 所構(gòu)成的銳二面角的余弦值.
所構(gòu)成的銳二面角的余弦值.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com