
【題目】在二項式![]() 的展開式中,前三項系數的絕對值成等差數列。
的展開式中,前三項系數的絕對值成等差數列。
(1)求展開式的第四項;
(2)求展開式的常數項;
(3)求展開式中各項的系數和.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】試題分析:(1)根據展開式的通項為![]() ,結合前三項系數的絕對值成等差數列,求得
,結合前三項系數的絕對值成等差數列,求得![]() ,從而求得展開式的第四項;(2)在展開式中,令
,從而求得展開式的第四項;(2)在展開式中,令![]() 的冪指數等于零,求得
的冪指數等于零,求得![]() 的值,代入通項公式可得常數項;(3)在二項式
的值,代入通項公式可得常數項;(3)在二項式![]() 的展開式中,令
的展開式中,令![]() ,可得各項系數和.
,可得各項系數和.
試題解析:展開式的通項為![]() ,r=0,1,2,…,n
,r=0,1,2,…,n
由已知:![]() 成等差數列,
成等差數列,
∴ ![]() ,∴ n=8 ,
,∴ n=8 ,![]() .
.
(1)令![]() ,
,![]() ,
,
(2)令![]() ,得
,得![]() ,
,![]() ,
,
(3)令x=1,各項系數和為 ![]() .
.
【方法點晴】本題主要考查二項展開式定理的通項與系數,屬于簡單題. 二項展開式定理的問題也是高考命題熱點之一,關于二項式定理的命題方向比較明確,主要從以下幾個方面命題:(1)考查二項展開式的通項公式![]() ;(可以考查某一項,也可考查某一項的系數)(2)考查各項系數和和各項的二項式系數和;(3)二項展開式定理的應用.
;(可以考查某一項,也可考查某一項的系數)(2)考查各項系數和和各項的二項式系數和;(3)二項展開式定理的應用.


科目:高中數學 來源: 題型:
【題目】如圖,在直四棱柱![]() 中,底面
中,底面![]() 為等腰梯形,
為等腰梯形,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
![]()
![]() 分別是
分別是![]()
![]()
![]() 的中點.
的中點.
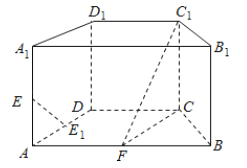
(1)證明:直線![]() 平面
平面![]() ;
;
(2)求直線![]() 與面
與面![]() 所成角的大小;
所成角的大小;
(3)求二面角![]() 的平面角的余弦值.
的平面角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某網店經營的一種商品進行進價是每件10元,根據一周的銷售數據得出周銷售量![]() (件)與單價
(件)與單價![]() (元)之間的關系如下圖所示,該網店與這種商品有關的周開支均為25元.
(元)之間的關系如下圖所示,該網店與這種商品有關的周開支均為25元.

(1)根據周銷售量圖寫出![]() (件)與單價
(件)與單價![]() (元)之間的函數關系式;
(元)之間的函數關系式;
(2)寫出利潤![]() (元)與單價
(元)與單價![]() (元)之間的函數關系式;當該商品的銷售價格為多少元時,周利潤最大?并求出最大周利潤.
(元)之間的函數關系式;當該商品的銷售價格為多少元時,周利潤最大?并求出最大周利潤.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知雙曲線C的中心在原點,拋物線![]() 的焦點是雙曲線C的一個焦點,且雙曲線過點
的焦點是雙曲線C的一個焦點,且雙曲線過點![]() .
.
(Ⅰ)求雙曲線的方程;
(Ⅱ)設直線![]() 與雙曲線C交于A,B兩點,試問:k為何值時,
與雙曲線C交于A,B兩點,試問:k為何值時,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
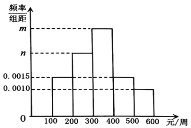
【題目】某網購平臺為了解某市居民在該平臺的消費情況,從該市使用其平臺且每周平均消費額超過100元的人員中隨機抽取了100名,并繪制右圖所示頻率分布直方圖,已知中間三組的人數可構成等差數列.
(1)求![]() 的值;
的值;
(2)分析人員對抽取對象每周的消費金額y與年齡x進一步分析,發現他們線性相關,得到回歸方程![]() .已知100名使用者的平均年齡為38歲,試判斷一名年齡為22歲的年輕人每周的平均消費金額為多少.(同一組數據用該區間的中點值代替)
.已知100名使用者的平均年齡為38歲,試判斷一名年齡為22歲的年輕人每周的平均消費金額為多少.(同一組數據用該區間的中點值代替)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】定義在![]() 上的函數
上的函數![]() ,如果滿足:對任意
,如果滿足:對任意![]() ,存在常數
,存在常數![]() ,都有
,都有![]() 成立,則稱
成立,則稱![]() 是
是![]() 上的有界函數,其中
上的有界函數,其中![]() 稱為函數
稱為函數![]() 的一個上界.已知函數
的一個上界.已知函數![]() ,
, ![]() .
.
(1)若函數![]() 為奇函數,求實數
為奇函數,求實數![]() 的值;
的值;
(2)在(1)的條件下,求函數![]() 在區間
在區間![]() 上的所有上界構成的集合;
上的所有上界構成的集合;
(3)若函數![]() 在
在![]() 上是以3為上界的有界函數,求實數
上是以3為上界的有界函數,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
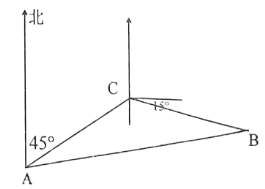
【題目】宿州泗縣石龍湖國家濕地公園是保存完好的典型濕地生態系統,具有得天獨厚的旅游資源.某日一游船在湖上游玩航行中突然遇險,發出呼救信號,駐湖救援隊在![]() 處獲悉后,立即測出該游船在北偏東
處獲悉后,立即測出該游船在北偏東![]() 方向上,距離
方向上,距離![]() 有
有![]() 千米的
千米的![]() 處,并測得游船正沿東偏南
處,并測得游船正沿東偏南![]() 的方向,以
的方向,以![]() 千米/時的速度向湖心小島
千米/時的速度向湖心小島![]() 靠攏,救援艦艇立即以
靠攏,救援艦艇立即以![]() 千米/時的速度前去營救,若想用最短的時間營救游船,求艦艇的航行方向和所需時間.
千米/時的速度前去營救,若想用最短的時間營救游船,求艦艇的航行方向和所需時間.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設![]() .若滿射
.若滿射![]() ,滿足:對任意的
,滿足:對任意的![]() ,
,![]() ,則稱
,則稱![]() 為“和諧函數”.記
為“和諧函數”.記 ![]() ,
,![]() .設“和諧映射”
.設“和諧映射”![]() 為滿足條件:存在正整數
為滿足條件:存在正整數![]() ,使得(1)當
,使得(1)當![]() 時,若
時,若![]() ,
,![]() ,則
,則![]()
![]()
![]() ;(2)若
;(2)若![]() ,
,![]() ,則
,則![]() ,求
,求![]() 的最大可能值.
的最大可能值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知集合![]() ,其中
,其中![]() ,
,![]() 是函數
是函數![]() 定義城內任意不相等的兩個實數.
定義城內任意不相等的兩個實數.
(1)若![]() ,同時
,同時![]() ,求證:
,求證:![]() ;
;
(2)判斷![]() 是否在集合A中,并說明理由;
是否在集合A中,并說明理由;
(3)設函數![]() 的定義域為B,函數
的定義域為B,函數![]() 的值域為C.函數
的值域為C.函數![]() 滿足以下3個條件:
滿足以下3個條件:
①![]() ,②
,②![]() ,③
,③![]() .試確定一個滿足以上3個條件的函數
.試確定一個滿足以上3個條件的函數![]() 要對滿足的條件進行說明).
要對滿足的條件進行說明).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com