
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,過焦點且垂直于長軸的弦長為
,過焦點且垂直于長軸的弦長為![]() .
.
(1)已知點![]() 是橢圓上兩點,點
是橢圓上兩點,點![]() 為橢圓的上頂點,
為橢圓的上頂點,![]() 的重心恰好是橢圓的右焦點
的重心恰好是橢圓的右焦點![]() ,求
,求![]() 所
所
在直線的斜率;
(2)過橢圓的右焦點![]() 作直線
作直線![]() ,直線
,直線![]() 與橢圓分別交于點
與橢圓分別交于點![]() ,直線
,直線![]() 與橢圓分別交于點
與橢圓分別交于點![]() ,
,
且![]() ,求四邊形
,求四邊形![]() 的面積
的面積![]() 最小時直線
最小時直線![]() 的方程.
的方程.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]()
【解析】
試題分析:(1)由橢圓的離心率為![]() ,過焦點且垂直于長軸的弦長為
,過焦點且垂直于長軸的弦長為![]() ,列出方程組求出
,列出方程組求出![]() ,
,![]() ,由此能求出橢圓方程為
,由此能求出橢圓方程為![]() ,由重心公式得
,由重心公式得![]() ,
,![]() ,由此結合點差法能求出直線
,由此結合點差法能求出直線![]() 的斜率;(2)設
的斜率;(2)設![]() ,
,![]() ,
,![]() ,
,![]() ,由題意推導出
,由題意推導出![]() ,若直線
,若直線![]() 中有一條斜率不存在,求出四邊形
中有一條斜率不存在,求出四邊形![]() 的面積為
的面積為![]() ;若直線
;若直線![]() ,
,![]() 的斜率存在,設直線
的斜率存在,設直線![]() 的方程為
的方程為![]() ,
,![]() ,與橢圓方程聯立,得
,與橢圓方程聯立,得![]() ,由此利用韋達定理、弦長公式求出
,由此利用韋達定理、弦長公式求出![]() ,同理可求得
,同理可求得![]() ,由此能求出四邊形
,由此能求出四邊形![]() 的面積
的面積![]() 的最小值及此時直線
的最小值及此時直線![]() 的方程.
的方程.
試題解析:(1)由題意:![]() ,
,![]() ,解得
,解得![]() ,
,
所求橢圓的方程為![]() .
.
設![]() ,∵
,∵![]() ,∴
,∴![]() ,根據題意
,根據題意![]() ,
,![]() ,
,
即![]() ,
,![]() .
.
由![]() ①,
①,![]() ②
②
①![]() ②得
②得![]() ,
,
∴![]() .
.
(2)設![]() ,
,![]() ,
,![]() ,
,![]() ,
,
則由題意:![]() ,
,
即![]()
整理得:![]() ,
,
即![]() ,所以
,所以![]() .
.
①若直線![]() 中有一條斜率不存在,不妨設
中有一條斜率不存在,不妨設![]() 的斜率不存在,則
的斜率不存在,則![]() 軸,
軸,
所以![]() ,
,![]() ,
,
故四邊形![]() 的面積
的面積![]() .
.
②若直線![]() 的斜率存在,設直線
的斜率存在,設直線![]() 的方程為:
的方程為:![]() ,
,
則由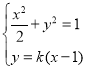 ,得
,得![]() ,
,
則![]() ,
,![]() ,
,
![]()
![]() ,
,
同理可求得,![]() ,故四邊形
,故四邊形![]() 的面積:
的面積:
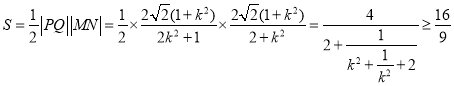
(當![]() 取“
取“![]() ”),
”),
此時,四邊形![]() 面積
面積![]() 的最小值為
的最小值為![]() ,
,
所以直線![]() 方程為:
方程為:![]() 或
或![]() .
.


科目:高中數學 來源: 題型:
【題目】明代商人程大位在公元1592年編撰完成《算法統宗》一書.書中有如下問題:“今有女子善織,初日遲,次日加倍,第三日轉速倍增,第四日又倍增,織成絹六丈七尺五寸.問各日織若干?”意思是:“有一位女子善于織布,第一天由于不熟悉有點慢,第二天起每天織的布都是前一天的2倍,已知她前四天共織布6丈7尺5寸,問這位女子每天織布多少?”根據文中的已知條件,可求得該女了第一天織布________尺,若織布一周(7天),共織________尺.(其中1丈為10尺,1尺為10寸)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 過點
過點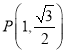 ,設它的左、右焦點分別為
,設它的左、右焦點分別為![]() 、
、![]() ,左頂點為
,左頂點為![]() ,上頂點為
,上頂點為![]() ,且滿足
,且滿足![]() .
.
(Ⅰ)求橢圓![]() 的標準方程和離心率;
的標準方程和離心率;
(Ⅱ)過點![]() 作不與
作不與![]() 軸垂直的直線交橢圓
軸垂直的直線交橢圓![]() 于
于![]() 、
、![]() (異于點
(異于點![]() )兩點,試判斷
)兩點,試判斷![]() 的大小是否為定值,并說明理由.
的大小是否為定值,并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下圖是某校某班44名同學的某次考試的物理成績y和數學成績x的散點圖:
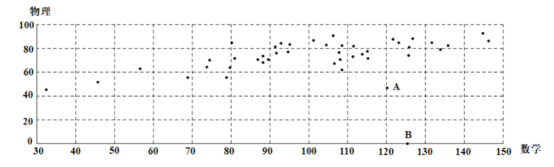
根據散點圖可以看出y與x之間有線性相關關系,但圖中有兩個異常點A,B.經調查得知,A考生由于重感冒導致物理考試發揮失常,B生因故未能參加物理考試.為了使分析結果更科學準確,剔除這兩組數據后,對剩下的數據作處理,得到一些統計量的值:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,其中
,其中![]() ,
,![]() 分別表示這42名同學的數學成績、物理成績,
分別表示這42名同學的數學成績、物理成績,![]() .y與x的相關系數
.y與x的相關系數![]() .
.
(1)若不剔除A、B兩名考生的數據,用44數據作回歸分析,設此時y與x的相關系數為![]() ,試判斷
,試判斷![]() 與r的大小關系,并說明理由;
與r的大小關系,并說明理由;
(2)求y關于x的線性回歸方程(系數精確到![]() ),并估計如果B考生參加了這次物理考試(已知B考生的數學成績為125分),物理成績是多少?(精確到個位).
),并估計如果B考生參加了這次物理考試(已知B考生的數學成績為125分),物理成績是多少?(精確到個位).
附:回歸方程![]() 中,
中, .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
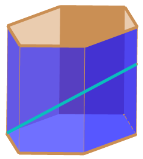
【題目】在我國瓷器的歷史上六棱形的瓷器非常常見,因為六、八是中國人的吉利數字,所以好多瓷器都做成六棱形和八棱形.數學李老師有一個正六棱柱形狀的筆筒,如圖,底面邊長為![]() ,高為
,高為![]() (底部及筒壁厚度忽略不計).一根長度為
(底部及筒壁厚度忽略不計).一根長度為![]() 的圓鐵棒
的圓鐵棒![]() (粗細忽略不計)斜放在筆筒內部,
(粗細忽略不計)斜放在筆筒內部,![]() 的一端置于正六棱柱某一側棱的底端,另一端置于和該側棱正對的側棱上.一位小朋友玩耍時,向筆筒內注水,恰好將圓鐵棒淹沒,又將一個圓球放在筆筒口,球面又恰好接觸水面,則球的表面積為______
的一端置于正六棱柱某一側棱的底端,另一端置于和該側棱正對的側棱上.一位小朋友玩耍時,向筆筒內注水,恰好將圓鐵棒淹沒,又將一個圓球放在筆筒口,球面又恰好接觸水面,則球的表面積為______![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com