
【題目】已知拋物線C:![]() =2px經過點
=2px經過點![]() (1,2).過點Q(0,1)的直線l與拋物線C有兩個不同的交點A,B,且直線PA交y軸于M,直線PB交y軸于N.
(1,2).過點Q(0,1)的直線l與拋物線C有兩個不同的交點A,B,且直線PA交y軸于M,直線PB交y軸于N.
(Ⅰ)求直線l的斜率的取值范圍;
(Ⅱ)設O為原點,![]() ,
,![]() ,求證:
,求證:![]() 為定值.
為定值.
【答案】(1) 取值范圍是(-∞,-3)∪(-3,0)∪(0,1)
(2)證明過程見解析
【解析】分析:(1)先確定p,再設直線方程,與拋物線聯立,根據判別式大于零解得直線l的斜率的取值范圍,最后根據PA,PB與y軸相交,舍去k=3,(2)先設A(x1,y1),B(x2,y2),與拋物線聯立,根據韋達定理可得![]() ,
,![]() .再由
.再由![]() ,
,![]() 得
得![]() ,
,![]() .利用直線PA,PB的方程分別得點M,N的縱坐標,代入化簡
.利用直線PA,PB的方程分別得點M,N的縱坐標,代入化簡![]() 可得結論.
可得結論.
詳解:解:(Ⅰ)因為拋物線y2=2px經過點P(1,2),
所以4=2p,解得p=2,所以拋物線的方程為y2=4x.
由題意可知直線l的斜率存在且不為0,
設直線l的方程為y=kx+1(k≠0).
由![]() 得
得![]() .
.
依題意![]() ,解得k<0或0<k<1.
,解得k<0或0<k<1.
又PA,PB與y軸相交,故直線l不過點(1,-2).從而k≠-3.
所以直線l斜率的取值范圍是(-∞,-3)∪(-3,0)∪(0,1).
(Ⅱ)設A(x1,y1),B(x2,y2).
由(I)知![]() ,
,![]() .
.
直線PA的方程為y–2=![]() .
.
令x=0,得點M的縱坐標為![]() .
.
同理得點N的縱坐標為![]() .
.
由![]() ,
,![]() 得
得![]() ,
,![]() .
.
所以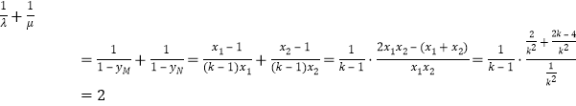 .
.
所以![]() 為定值.
為定值.


 第三學期贏在暑假系列答案
第三學期贏在暑假系列答案 學練快車道快樂假期暑假作業新疆人民出版社系列答案
學練快車道快樂假期暑假作業新疆人民出版社系列答案 浙大優學小學年級銜接導與練浙江大學出版社系列答案
浙大優學小學年級銜接導與練浙江大學出版社系列答案科目:高中數學 來源: 題型:
【題目】如圖,在四面體ABCD中,△ABC是等邊三角形,平面ABC⊥平面ABD,點M為棱AB的中點,AB=2,AD=![]() ,∠BAD=90°.
,∠BAD=90°.
(Ⅰ)求證:AD⊥BC;
(Ⅱ)求異面直線BC與MD所成角的余弦值;
(Ⅲ)求直線CD與平面ABD所成角的正弦值.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
: ![]() (
(![]() )的左右焦點分別為
)的左右焦點分別為![]() ,
, ![]() ,若橢圓上一點
,若橢圓上一點![]() 滿足
滿足![]() ,且橢圓
,且橢圓![]() 過點
過點![]() ,過點
,過點![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于兩點
交于兩點![]()
![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)過點![]() 作
作![]() 軸的垂線,交橢圓
軸的垂線,交橢圓![]() 于
于![]() ,求證:
,求證: ![]() ,
, ![]() ,
, ![]() 三點共線.
三點共線.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱柱ABC-![]() 中,
中,![]() 平面ABC,D,E,F,G分別為
平面ABC,D,E,F,G分別為![]() ,AC,
,AC,![]() ,
,![]() 的中點,AB=BC=
的中點,AB=BC=![]() ,AC=
,AC=![]() =2.
=2.

(Ⅰ)求證:AC⊥平面BEF;
(Ⅱ)求二面角B-CD-C1的余弦值;
(Ⅲ)證明:直線FG與平面BCD相交.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】以“你我中國夢,全民建小康”為主題、“社會主義核心價值觀”為主線,為了了解![]() 兩個地區的觀眾對2018年韓國平昌冬奧會準備工作的滿意程度,對
兩個地區的觀眾對2018年韓國平昌冬奧會準備工作的滿意程度,對![]() 地區的100名觀眾進行統計,統計結果如下:
地區的100名觀眾進行統計,統計結果如下:
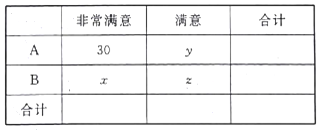
在被調查的全體觀眾中隨機抽取1名“非常滿意”的人是![]() 地區的概率為0.45,且
地區的概率為0.45,且![]() .
.
(Ⅰ)現從100名觀眾中用分層抽樣的方法抽取20名進行問卷調查,則應抽取“滿意”的![]() 地區的人數各是多少?
地區的人數各是多少?
(Ⅱ)在(Ⅰ)抽取的“滿意”的觀眾中,隨機選出3人進行座談,求至少有兩名是![]() 地區觀眾的概率?
地區觀眾的概率?
(Ⅲ)完成上述表格,并根據表格判斷是否有![]() 的把握認為觀眾的滿意程度與所在地區有關系?
的把握認為觀眾的滿意程度與所在地區有關系?
附: 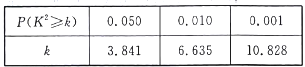 ,
, 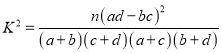 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了了解甲、乙兩個工廠生產的輪胎的寬度是否達標,分別從兩廠隨機各選取了![]() 個輪胎,將每個輪胎的寬度(單位:
個輪胎,將每個輪胎的寬度(單位: ![]() )記錄下來并繪制出如下的折線圖:
)記錄下來并繪制出如下的折線圖:
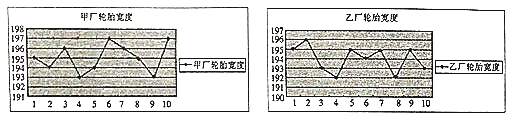
(1)分別計算甲、乙兩廠提供的![]() 個輪胎寬度的平均值;
個輪胎寬度的平均值;
(2)輪胎的寬度在![]() 內,則稱這個輪胎是標準輪胎.
內,則稱這個輪胎是標準輪胎.
(i)若從甲乙提供的![]() 個輪胎中隨機選取
個輪胎中隨機選取![]() 個,求所選的輪胎是標準輪胎的概率
個,求所選的輪胎是標準輪胎的概率![]() ;
;
(ii)試比較甲、乙兩廠分別提供的![]() 個輪胎中所有標準輪胎寬度的方差大小,根據兩廠的標準輪胎寬度的平均水平及其波動情況,判斷這兩個工廠哪個廠的輪胎相對更好?
個輪胎中所有標準輪胎寬度的方差大小,根據兩廠的標準輪胎寬度的平均水平及其波動情況,判斷這兩個工廠哪個廠的輪胎相對更好?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com