
【題目】隨著人口老齡化的到來,我國的勞動力人口在不斷減少,“延遲退休”已經(jīng)成為人們越來越關(guān)注的話題,為了解公眾對“延遲退休”的態(tài)度,某校課外研究性學(xué)習(xí)小組在某社區(qū)隨機(jī)抽取了50人進(jìn)行調(diào)查,將調(diào)查情況進(jìn)行整理后制成下表:
年齡 | [20,25) | [25,30) | [30,35) | [35,40) | [40,45) |
人數(shù) | 4 | 5 | 8 | 5 | 3 |
年齡 | [45,50) | [50,55) | [55,60) | [60,65) | [65,70) |
人數(shù) | 6 | 7 | 3 | 5 | 4 |
經(jīng)調(diào)查年齡在[25,30),[55,60)的被調(diào)查者中贊成“延遲退休”的人數(shù)分別是3人和2人.現(xiàn)從這兩組的被調(diào)查者中各隨機(jī)選取2人,進(jìn)行跟蹤調(diào)查.
(I)求年齡在[25,30)的被調(diào)查者中選取的2人都贊成“延遲退休”的概率;
(II)若選中的4人中,不贊成“延遲退休”的人數(shù)為![]() ,求隨機(jī)變量
,求隨機(jī)變量![]() 的分布列和數(shù)學(xué)期望.
的分布列和數(shù)學(xué)期望.


| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖, ![]() 是半圓
是半圓![]() 的直徑,
的直徑, ![]() 是半圓
是半圓![]() 上除
上除![]() 、
、![]() 外的一個動點(diǎn),
外的一個動點(diǎn), ![]() 垂直于半圓
垂直于半圓![]() 所在的平面,
所在的平面, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
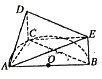
(1)證明:平面![]() 平面
平面![]() ;
;
(2)當(dāng)三棱錐![]() 體積最大時,求二面角
體積最大時,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
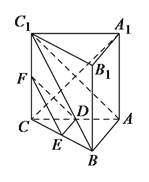
【題目】如圖,在三棱柱![]() 中,
中,![]() 底面
底面![]() ,
,![]()
![]() ,
,![]() 、
、![]() 分別是棱
分別是棱![]() 、
、![]() 的中點(diǎn).
的中點(diǎn).
(Ⅰ)求證:![]() 平面
平面![]() .
.
(Ⅱ)若線段![]() 上的點(diǎn)
上的點(diǎn)![]() 滿足平面
滿足平面![]() 平面
平面![]() ,試確定點(diǎn)
,試確定點(diǎn)![]() 的位置,并說明理由.
的位置,并說明理由.
(Ⅲ)證明:![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)=|cosx|sinx,給出下列四個說法:
①f(x)為奇函數(shù); ②f(x)的一條對稱軸為x= ![]() ;
;
③f(x)的最小正周期為π; ④f(x)在區(qū)間[﹣ ![]() ,
, ![]() ]上單調(diào)遞增;
]上單調(diào)遞增;
⑤f(x)的圖象關(guān)于點(diǎn)(﹣ ![]() ,0)成中心對稱.
,0)成中心對稱.
其中正確說法的序號是 .
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】對某地區(qū)兒童的身高與體重的一組數(shù)據(jù),我們用兩種模型①![]() ,②
,②![]() 擬合,得到回歸方程分別為
擬合,得到回歸方程分別為![]() ,
, ![]() ,作殘差分析,如表:
,作殘差分析,如表:
身高 | 60 | 70 | 80 | 90 | 100 | 110 |
體重 | 6 | 8 | 10 | 14 | 15 | 18 |
| 0.41 | 0.01 | 1.21 | -0.19 | 0.41 | |
| -0.36 | 0.07 | 0.12 | 1.69 | -0.34 | -1.12 |
(Ⅰ)求表中空格內(nèi)的值;
(Ⅱ)根據(jù)殘差比較模型①,②的擬合效果,決定選擇哪個模型;
(Ⅲ)殘差大于![]() 的樣本點(diǎn)被認(rèn)為是異常數(shù)據(jù),應(yīng)剔除,剔除后對(Ⅱ)所選擇的模型重新建立回歸方程.
的樣本點(diǎn)被認(rèn)為是異常數(shù)據(jù),應(yīng)剔除,剔除后對(Ⅱ)所選擇的模型重新建立回歸方程.
(結(jié)果保留到小數(shù)點(diǎn)后兩位)
附:對于一組數(shù)據(jù)![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘法估計分別為
的斜率和截距的最小二乘法估計分別為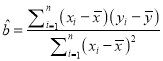 ,
, ![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知點(diǎn)![]() ,⊙
,⊙![]() .
.
(Ⅰ)當(dāng)直線![]() 過點(diǎn)
過點(diǎn)![]() 且與圓心
且與圓心![]() 的距離為
的距離為![]() 時,求直線
時,求直線![]() 的方程.
的方程.
(Ⅱ)設(shè)過點(diǎn)![]() 的直線與⊙
的直線與⊙![]() 交于
交于![]() ,
, ![]() 兩點(diǎn),且
兩點(diǎn),且![]() ,求以線段
,求以線段![]() 為直徑的圓的方程.
為直徑的圓的方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)=ax+ ![]() (a>1)
(a>1)
(1)證明:函數(shù)f(x)在(﹣1,+∞)上為增函數(shù);
(2)用反證法證明f(x)=0沒有負(fù)數(shù)根.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,棱柱ABC﹣A1B1C1的側(cè)面BCC1B1是菱形,B1C⊥A1B 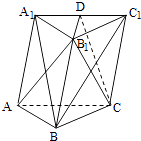
(1)證明:平面AB1C⊥平面A1BC1;
(2)設(shè)D是A1C1上的點(diǎn),且A1B∥平面B1CD,求A1D:DC1的值.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com