
【題目】已知函數f(x)=|cosx|sinx,給出下列四個說法:
①f(x)為奇函數; ②f(x)的一條對稱軸為x= ![]() ;
;
③f(x)的最小正周期為π; ④f(x)在區間[﹣ ![]() ,
, ![]() ]上單調遞增;
]上單調遞增;
⑤f(x)的圖象關于點(﹣ ![]() ,0)成中心對稱.
,0)成中心對稱.
其中正確說法的序號是 .
【答案】①②④
【解析】解:函數f(x)=|cosx|sinx= 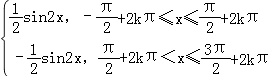 (k∈Z),
(k∈Z),
①、f(﹣x)=|cos(﹣x)|sin(﹣x)=﹣|cosx|sinx=﹣f(x),
則f(x)是奇函數,①正確;
②、∵f(π﹣x)=|cos(π﹣x)|sin(π﹣x)=|﹣cosx|sinx=f(x),
∴f(x)的一條對稱軸為x= ![]() ,②正確;
,②正確;
③、∵f(π+x)=|cos(π+x)|sin(π+x)=|﹣cosx|(﹣sinx)=﹣f(x)≠f(x),
∴f(x)的最小正周期不是π,③不正確;
④、∵x∈[﹣ ![]() ,
, ![]() ],∴f(x)=|cosx|sinx=
],∴f(x)=|cosx|sinx= ![]() sin2x,且2x∈[﹣
sin2x,且2x∈[﹣ ![]() ,
, ![]() ],
],
∴f(x)在區間[﹣ ![]() ,
, ![]() ]上單調遞增,④正確;
]上單調遞增,④正確;
⑤、∵f(﹣π﹣x)=|cos(﹣π﹣x)|sin(﹣π﹣x)=|﹣cosx|sinx=f(x)≠﹣f(x),
∴f(x)的圖象不關于點(﹣ ![]() ,0)成中心對稱,⑤不正確;
,0)成中心對稱,⑤不正確;
所以答案是:①②④.
【考點精析】解答此題的關鍵在于理解命題的真假判斷與應用的相關知識,掌握兩個命題互為逆否命題,它們有相同的真假性;兩個命題為互逆命題或互否命題,它們的真假性沒有關系.


科目:高中數學 來源: 題型:
【題目】某網站針對2015年中國好聲音歌手A,B,C三人進行網上投票,結果如下
觀眾年齡 | 支持A | 支持B | 支持C |
20歲以下 | 100 | 200 | 600 |
20歲以上(含20歲) | 100 | 100 | 400 |
(1)在所有參與該活動的人中,用分層抽樣的方法抽取n人,其中有6人支持A,求n的值.
(2)在支持C的人中,用分層抽樣的方法抽取5人作為一個總體,從這5人中任意選取2人,求恰有1人在20歲以下的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】平面內有向量 ![]() =(1,7),
=(1,7), ![]() =(5,1),
=(5,1), ![]() =(2,1),點X為直線OP上的一個動點.
=(2,1),點X為直線OP上的一個動點.
(1)當 ![]()
![]() 取最小值時,求
取最小值時,求 ![]() 的坐標;
的坐標;
(2)當點X滿足(1)的條件和結論時,求cos∠AXB的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(文)已知矩形ABB1A1是圓柱體的軸截面,O、O1分別是下底面圓和上底面圓的圓心,母線長與底面圓的直徑長之比為2:1,且該圓柱體的體積為32π,如圖所示. 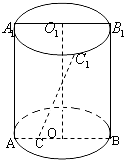
(1)求圓柱體的側面積S側的值;
(2)若C1是半圓弧 ![]() 的中點,點C在半徑OA上,且OC=
的中點,點C在半徑OA上,且OC= ![]() OA,異面直線CC1與BB1所成的角為θ,求sinθ的值.
OA,異面直線CC1與BB1所成的角為θ,求sinθ的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}的前n項和為Tn= ![]() n2﹣
n2﹣ ![]() n,且an+2+3log4bn=0(n∈N*)
n,且an+2+3log4bn=0(n∈N*)
(1)求{bn}的通項公式;
(2)數列{cn}滿足cn=anbn , 求數列{cn}的前n項和Sn;
(3)若cn≤ ![]() m2+m﹣1對一切正整數n恒成立,求實數m的取值范圍.
m2+m﹣1對一切正整數n恒成立,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖:已知四棱錐P﹣ABCD中,PD⊥平面ABCD,ABCD是正方形,E是PA的中點,求證: 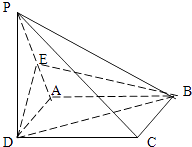
(1)PC∥平面EBD.
(2)平面PBC⊥平面PCD.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著人口老齡化的到來,我國的勞動力人口在不斷減少,“延遲退休”已經成為人們越來越關注的話題,為了解公眾對“延遲退休”的態度,某校課外研究性學習小組在某社區隨機抽取了50人進行調查,將調查情況進行整理后制成下表:
年齡 | [20,25) | [25,30) | [30,35) | [35,40) | [40,45) |
人數 | 4 | 5 | 8 | 5 | 3 |
年齡 | [45,50) | [50,55) | [55,60) | [60,65) | [65,70) |
人數 | 6 | 7 | 3 | 5 | 4 |
經調查年齡在[25,30),[55,60)的被調查者中贊成“延遲退休”的人數分別是3人和2人.現從這兩組的被調查者中各隨機選取2人,進行跟蹤調查.
(I)求年齡在[25,30)的被調查者中選取的2人都贊成“延遲退休”的概率;
(II)若選中的4人中,不贊成“延遲退休”的人數為![]() ,求隨機變量
,求隨機變量![]() 的分布列和數學期望.
的分布列和數學期望.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() 和直線
和直線![]() ,直線
,直線![]() ,
, ![]() 都經過圓
都經過圓![]() 外定點
外定點![]() .
.
(1)若直線![]() 與圓
與圓![]() 相切,求直線
相切,求直線![]() 的方程;
的方程;
(2)若直線![]() 與圓
與圓![]() 相交于
相交于![]() 兩點,與
兩點,與![]() 交于
交于![]() 點,且線段
點,且線段![]() 的中點為
的中點為![]() ,
,
求證: ![]() 為定值.
為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
: ![]() (
(![]() )過點
)過點![]() ,且離心率為
,且離心率為![]() ,過點
,過點![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于
交于![]() ,
, ![]() 兩點.
兩點.
(Ⅰ)求橢圓的![]() 的標準方程;
的標準方程;
(Ⅱ)已知![]() 為坐標原點,且
為坐標原點,且![]() ,求
,求![]() 面積的最大值以及此時直線
面積的最大值以及此時直線![]() 的方程.
的方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com