Question

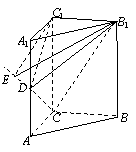
（08年黃岡中學三模）如圖，在直三棱柱ABC―A₁B₁C₁中， .

（Ⅰ）若D為AA₁中點，求證：平面B₁CD平面B₁C₁D；

（Ⅱ）若二面角B₁―DC―C₁的大小為60°，求AD的長.

 

 

Answer 1

解析：解法一：（Ⅰ）∵，∴，

又由直三棱柱性質知，∴平面ACC₁A₁.

∴……①

由D為中點可知，，∴

即……②

由①②可知平面B₁C₁D，又平面B₁CD，

故平面平面B₁C₁D.  

（Ⅱ）由（1）可知平面ACC₁A₁，如圖，

在面ACC₁A₁內過C₁作，

交CD或延長線或于E，連EB₁，

由三垂線定理可知為二面角B­₁―DC―C₁的平面角，

∴ 

由B₁C₁=2知，，設AD=x，則

∵的面積為1，

     ∴，解得，即

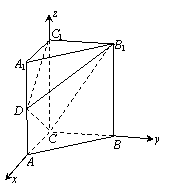
解法二：（Ⅰ）如圖，以C為原點，CA、CB、CC₁所在直線為x, y, z軸建立空間直角坐標系.

 則 C（0，0，0），A（1，0，0），B₁（0，2，2），C₁（0，0，2），D（1，0，1）.

即

由，得；

由，得；

又，∴平面B₁C₁D.

又平面B₁CD，

∴平面平面B₁C₁D.  

（Ⅱ）設AD=a，則D點坐標為（1，0，a），，

設平面B₁CD的法向量為. 則由，令z= -1，

得，又平面C₁DC的法向量為，則由，即，故