
【題目】已知等比數列![]() 中,
中, ![]() ,且
,且![]() .
.
(1)求數列![]() 的通項公式;
的通項公式;
(2)求數列![]() 的前
的前![]() 項和
項和![]() .
.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】試題分析:(1)根據題意列出關于首項![]() ,公比
,公比![]() 的方程組,解得
的方程組,解得![]() 、
、![]() 的值,即可求數列
的值,即可求數列![]() 的通項公式;(2)由(1)可得
的通項公式;(2)由(1)可得![]() ,利用錯位相減法即可得到數列的和.
,利用錯位相減法即可得到數列的和.
試題解析:(1)![]() ,即
,即![]() .
.
(2) ![]() , ①
, ①
(i)當![]() 時,
時, ![]() ;(ii)當
;(ii)當![]() 時,
時, ![]() , ②
, ②
①-②得, ![]() ,整理得
,整理得![]() ,由(i)(ii)得
,由(i)(ii)得![]() .
.
【 方法點睛】本題主要考查等比數列的通項與求和公式以及錯位相減法求數列的的前![]() 項和,屬于中檔題.一般地,如果數列
項和,屬于中檔題.一般地,如果數列![]() 是等差數列,
是等差數列, ![]() 是等比數列,求數列
是等比數列,求數列![]() 的前
的前![]() 項和時,可采用“錯位相減法”求和,一般是和式兩邊同乘以等比數列
項和時,可采用“錯位相減法”求和,一般是和式兩邊同乘以等比數列![]() 的公比,然后作差求解, 在寫出“
的公比,然后作差求解, 在寫出“”與“
![]() ” 的表達式時應特別注意將兩式“錯項對齊”以便下一步準確寫出“
” 的表達式時應特別注意將兩式“錯項對齊”以便下一步準確寫出“![]() ”的表達式.
”的表達式.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】如圖,四棱錐P-ABCD中,PA⊥平面ABCD,底面ABCD是邊長為2的正方形,
PA=AD,F為PD的中點.
(1)求證:AF⊥平面PDC;
(2)求直線AC與平面PCD所成角的大小.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設△ABC的內角A、B、C所對的邊長分別為a、b、c,且acos B=3,bsin A=4.
(1)求邊長a;
(2)若△ABC的面積S=10,求△ABC的周長l.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列四個命題中正確的是( ).
①若一個平面內的兩條直線與另一個平面都平行,那么這兩個平面互相平行;
②若一條直線和兩個平行平面中的一個平面垂直,那么這條直線也和另一個平面垂直;
③若一條直線和兩個互相垂直的平面中的一個平面垂直,那么這條直線一定平行于另一個平面;
④若兩個平面垂直,那么,一個平面內與它們的交線不垂直的直線與另一個平面也不垂直.
A. ②和④ B. ②和③ C. ③和④ D. ①和②
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】遼寧號航母紀念章從2012年10月5日起開始上市,通過市場調查,得到該紀念章每![]() 枚的市場價
枚的市場價![]() (單位:元)與上市時間
(單位:元)與上市時間![]() (單位:天)的數據如下:
(單位:天)的數據如下:
上市時間 |
|
|
|
市場價 |
|
|
|
(1)根據上表數據,從下列函數中選取一個恰當的函數描述遼寧號航母紀念章的市場價![]() 與上市時間
與上市時間![]() 的變化關系:①
的變化關系:①![]() ;②
;②![]() ;③
;③![]() ;
;
(2)利用你選取的函數,求遼寧號航母紀念章市場價最低時的上市天數及最低的價格;
(3)設你選取的函數為![]() ,若對任意實數
,若對任意實數![]() ,關于
,關于![]() 的方程
的方程![]() 恒有個想異實數根,求
恒有個想異實數根,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知,如圖, ![]() ,圖中的一系列圓是圓心分別為
,圖中的一系列圓是圓心分別為![]() ,
, ![]() 的兩組同心圓,每組同心圓的半徑依次為
的兩組同心圓,每組同心圓的半徑依次為![]() ,
, ![]() ,
, ![]()
![]() ,
,
按“加![]() ”依次遞增,點
”依次遞增,點![]() 是某兩圓的一個交點,設:
是某兩圓的一個交點,設:
以![]() ,
, ![]() 為焦點,且過點
為焦點,且過點![]() 的橢圓為
的橢圓為![]() ;
;
以![]() ,
, ![]() 為焦點,且過點
為焦點,且過點![]() 的雙曲線為
的雙曲線為![]() ,
,
則
(![]() )雙曲線
)雙曲線![]() 離心率
離心率![]() __________.
__________.
(![]() )若以
)若以![]() 為
為![]() 軸正方向,線段
軸正方向,線段![]() 中點為坐標原點建立平面直角坐標系,則
中點為坐標原點建立平面直角坐標系,則
橢圓![]() 方程為__________.
方程為__________.
(3)雙曲線![]() 漸近線方程為__________.
漸近線方程為__________.
(4)在兩組同心圓的交點中,在橢圓![]() 上的點共__________個.
上的點共__________個.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在每年的3月份,濮陽市政府都會發動市民參與到植樹綠化活動中去林業管理部門為了保證樹苗的質量都會在植樹前對樹苗進行檢測,現從甲、乙兩種樹苗中各抽測了![]() 株樹苗,量出它們的高度如下(單位:厘米),
株樹苗,量出它們的高度如下(單位:厘米),
甲:37,21,31,20,29,19,32,23,25,33;
乙:10,30,47,27,46,14,26,10,44,46.
(1)畫出兩組數據的莖葉圖并根據莖葉圖對甲、乙兩種樹苗的高度作比較,寫出兩個統計結論;
(2)設抽測的![]() 株甲種樹苗高度平均值為
株甲種樹苗高度平均值為![]() ,將這
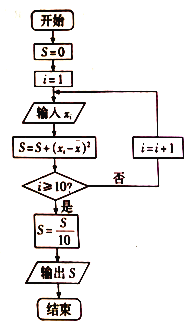
,將這![]() 株樹苗的高度依次輸人,按程序框(如圖)進行運算,問輸出的
株樹苗的高度依次輸人,按程序框(如圖)進行運算,問輸出的![]() 大小為多少?并說明
大小為多少?并說明![]() 的統計學意義,
的統計學意義,
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com