
【題目】從分別寫有![]() 的
的![]() 張卡片中隨機抽取
張卡片中隨機抽取![]() 張,放回后再隨機抽取
張,放回后再隨機抽取![]() 張,則抽得的第一張卡片,上的數不大于第二張卡片上的數的概率為( )
張,則抽得的第一張卡片,上的數不大于第二張卡片上的數的概率為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】
分析:基本事件總數n=5×5=25,利用列舉法求出抽得的第一張卡片上的數不小于第二張卡片上的數包含的基本事件有15個,由此能求出抽得的第一張卡片上的數不大于第二張卡片上的數的概率.
詳解:從分別寫有1,2,3,4,5的5張卡片中隨機抽取1張,放回后再隨機抽取1張,
基本事件總數n=5×5=25,
抽得的第一張卡片上的數不大于第二張卡片上的數包含的基本事件有15個,分別為:
(1,2),(2,3),(1,3),(3,4),(2,4),(1,4),(4,5),(3,5),
(2,5),(1,5),(5,6),(4,6),(3,6),(2,6),(1,6),
則抽得的第一張卡片上的數不小于第二張卡片上的數的概率為p=![]()
故選:D.


 能力評價系列答案
能力評價系列答案科目:高中數學 來源: 題型:
【題目】如圖,某公園摩天輪的半徑為![]() ,圓心距地面的高度為
,圓心距地面的高度為![]() ,摩天輪做勻速轉動,每
,摩天輪做勻速轉動,每![]() 轉一圈,摩天輪上的點
轉一圈,摩天輪上的點![]() 的起始位置在最低點處.
的起始位置在最低點處.
(1)已知在時刻![]() 時
時![]() 距離地面的高度
距離地面的高度![]() ,(其中
,(其中![]() ),求
),求![]() 時
時![]() 距離地面的高度;
距離地面的高度;
(2)當離地面![]() 以上時,可以看到公園的全貌,求轉一圈中有多少時間可以看到公園的全貌?
以上時,可以看到公園的全貌,求轉一圈中有多少時間可以看到公園的全貌?

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在底面是菱形的四棱錐P﹣ABCD中, ![]() E、F分別為PD、AB的中點,△PAB為等腰直角三角形,PA⊥平面ABCD,PA=1.
E、F分別為PD、AB的中點,△PAB為等腰直角三角形,PA⊥平面ABCD,PA=1.

(1)求證:直線AE∥平面PFC;
(2)求證:PB⊥FC.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設![]() 為雙曲線
為雙曲線![]() :
: ![]() 的右焦點,過坐標原點的直線依次與雙曲線
的右焦點,過坐標原點的直線依次與雙曲線![]() 的左、右支交于點
的左、右支交于點![]() ,若
,若![]() ,
, ![]() ,則該雙曲線的離心率為( )
,則該雙曲線的離心率為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】![]() ,設雙曲線的左焦點為
,設雙曲線的左焦點為![]() ,連接
,連接![]() ,由對稱性可知,
,由對稱性可知, ![]() 為矩形,且
為矩形,且![]() ,故
,故![]() ,故選B.
,故選B.
【 方法點睛】本題主要考查雙曲線的定義及離心率,屬于難題.離心率的求解在圓錐曲線的考查中是一個重點也是難點,一般求離心率有以下幾種情況:①直接求出![]() ,從而求出
,從而求出![]() ;②構造
;②構造![]() 的齊次式,求出
的齊次式,求出![]() ;③采用離心率的定義以及圓錐曲線的定義來求解;④根據圓錐曲線的統一定義求解.
;③采用離心率的定義以及圓錐曲線的定義來求解;④根據圓錐曲線的統一定義求解.
【題型】單選題
【結束】
12
【題目】點![]() 到點
到點![]() ,
, ![]() 及到直線
及到直線![]() 的距離都相等,如果這樣的點恰好只有一個,那么實數
的距離都相等,如果這樣的點恰好只有一個,那么實數![]() 的值是( )
的值是( )
A. ![]() B.
B. ![]() C.
C. ![]() 或
或![]() D.
D. ![]() 或
或![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 是平行四邊形,
是平行四邊形, ![]() ,側面
,側面![]() 底面
底面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分別為
分別為![]() ,
, ![]() 的中點,點
的中點,點![]() 在線段
在線段![]() 上.
上.

(1)求證: ![]() 平面
平面![]() ;
;
(2)若直線![]() 與平面
與平面![]() 所成的角和直線
所成的角和直線![]() 與平面
與平面![]() 所成的角相等,求
所成的角相等,求![]() 的值.
的值.
【答案】(1)證明見解析;(2) ![]() .
.
【解析】試題分析:
(Ⅰ)在平行四邊形![]() 中,由條件可得
中,由條件可得![]() ,進而可得
,進而可得![]() 。由側面
。由側面![]() 底面
底面![]() ,得
,得![]() 底面
底面![]() ,故得
,故得![]() ,所以可證得
,所以可證得![]() 平面
平面![]() .(Ⅱ)先證明平面
.(Ⅱ)先證明平面![]() 平面
平面![]() ,由面面平行的性質可得
,由面面平行的性質可得![]() 平面
平面![]() .(Ⅲ)建立空間直角坐標系,通過求出平面的法向量,根據線面角的向量公式可得
.(Ⅲ)建立空間直角坐標系,通過求出平面的法向量,根據線面角的向量公式可得![]() 。
。
試題解析:
(Ⅰ)證明:在平行四邊形![]() 中,
中,
∵![]() ,
, ![]() ,
, ![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
, ![]() 分別為
分別為![]() ,
, ![]() 的中點,
的中點,
∴![]() ,
,
∴![]() ,
,
∵側面![]() 底面
底面![]() ,且
,且![]() ,
,
∴![]() 底面
底面![]() ,
,
又![]() 底面
底面![]() ,
,
∴![]() ,
,
又![]() ,
, ![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
(Ⅱ)證明:∵![]() 為
為![]() 的中點,
的中點, ![]() 為
為![]() 的中點,
的中點,
∴![]() ,
,
又![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
同理![]() 平面
平面![]() ,
,
又![]() ,
, ![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
(Ⅲ)解:由![]() 底面
底面![]() ,
, ![]() ,可得
,可得![]() ,
, ![]() ,
, ![]() 兩兩垂直,
兩兩垂直,
建立如圖空間直角坐標系![]() ,
,

則![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
所以![]() ,
, ![]() ,
, ![]() ,
,
設![]() ,則
,則![]() ,
,
∴![]() ,
, ![]() ,
,
易得平面![]() 的法向量
的法向量![]() ,
,
設平面![]() 的法向量為
的法向量為![]() ,則:
,則:
由![]() ,得
,得![]() ,
,
令![]() ,得
,得![]() ,
,
∵直線![]() 與平面
與平面![]() 所成的角和此直線與平面
所成的角和此直線與平面![]() 所成的角相等,
所成的角相等,
∴![]() ,即
,即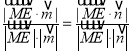 ,
,
∴![]() ,
,
解得![]() 或
或![]() (舍去),
(舍去),
故![]() .
.
點睛:用向量法確定空間中點的位置的方法
根據題意建立適當的空間直角坐標系,由條件確定有關點的坐標,運用共線向量用參數(參數的范圍要事先確定)確定出未知點的坐標,根據向量的運算得到平面的法向量或直線的方向向量,根據所給的線面角(或二面角)的大小進行運算,進而求得參數的值,通過與事先確定的參數的范圍進行比較,來判斷參數的值是否符合題意,進而得出點是否存在的結論。
【題型】解答題
【結束】
21
【題目】如圖,橢圓![]() 上的點到左焦點的距離最大值是
上的點到左焦點的距離最大值是![]() ,已知點
,已知點![]() 在橢圓上,其中
在橢圓上,其中![]() 為橢圓的離心率.
為橢圓的離心率.

(1)求橢圓的方程;
(2)過原點且斜率為![]() 的直線交橢圓于
的直線交橢圓于![]() 、
、![]() 兩點,其中
兩點,其中![]() 在第一象限,它在
在第一象限,它在![]() 軸上的射影為點
軸上的射影為點![]() ,直線
,直線![]() 交橢圓于另一點
交橢圓于另一點![]() .證明:對任意的
.證明:對任意的![]() ,點
,點![]() 恒在以線段
恒在以線段![]() 為直徑的圓內.
為直徑的圓內.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】等差數列{an}的前n項和為Sn,且![]() =9,S6=60.
=9,S6=60.
(I)求數列{an}的通項公式;
(II)若數列{bn}滿足bn+1﹣bn=![]() (n∈N+)且b1=3,求數列
(n∈N+)且b1=3,求數列![]() 的前n項和Tn.
的前n項和Tn.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com