Question

【題目】已知AB是⊙O的直徑，直線AF交⊙O于F（不與B重合），直線EC與⊙O相切于C，交AB于E，連接AC，且∠OAC=∠CAF，求證：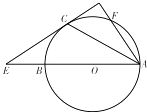

（1）AF⊥EC；
（2）若AE=5，AF=2，求AC．

Answer 1

【答案】
（1）證明：設EC與AF交于M，連接BC，則BC⊥AC，

因為直線EC與⊙O相切于C，

所以∠ACM=∠ABC，

因為∠OAC=∠CAF，

所以∠OAC+∠ABC=∠CAF+∠ACM=90°，

所以AF⊥EC

（2）解：連接CF，則∠MCF=∠MAC，∠ECB=∠OAC，

因為∠OAC=∠CAF，

所以∠ACE=∠AFC，

所以△ACE∽△AFC，

所以 ，

所以AC2=AEAF，

因為AE=5，AF=2，

所以AC= ．

【解析】（1）設EC與AF交于M，連接BC，則BC⊥AC，證明∠OAC+∠ABC=∠CAF+∠ACM=90°，即可證明AF⊥EC；（2）證明△ACE∽△AFC，可得AC2=AEAF，利用AE=5，AF=2，求AC．