【題目】在
中，角
、
、
所對的邊分別為
、
、
，
，當角取最大值時，的周長為
，則
__________．
【答案】3
【解析】分析：根據題意由正弦定理得出cosA＜0，A為鈍角，cosAcosC≠0，由兩角和的正弦函數公式，同角三角函數基本關系式可得出tanA=﹣3tanC，且tanC＞0；由已知及基本不等式求出B取得最大值，可得C=B=
，可求A，利用余弦定理可求a=
b，結合已知求得b的值，進而可求a的值．
詳解：△ABC中，
sinB=cos（B+C）sinC，
∴b=cos（B+C）c，即cosA=﹣
＜0，∴A為鈍角，
∴cosAcosC≠0；
由sinB=sin（A+C）=sinAcosC+cosAsinC=﹣2cosAsinC，
可得tanA=﹣3tanC，且tanC＞0，
=
當且僅當tanC=
時取等號；
∴B取得最大值時，c=b=1，此時C=B=．
∴A=
，由a2=b2+c2﹣2bccosA，可得：a=b，
∵三角形的周長為a+b+c=b +b+b=2
．解得：b=
，可得：a=b =3．
故答案為：3
陽光課堂課時優化作業系列答案科目：高中數學 來源： 題型：
【題目】下列說法：
①若集合
，
，則
；
②定義在
上的函數
， 若為奇函數，則必有
；
③方程
有兩個實根；
④存在
，
，使得
.
其中說法正確的序號是（ ）
A.②③B.②④
C.①②③D.②
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】為了解學生的身體素質情況，現從我校學生中隨機抽取10人進行體能測試，測試的分數（百分制）如莖葉圖所示.根據有關國家標準，成績不低于79分的為優秀，將頻率視為概率.
(1)另從我校學生中任取3人進行測試，求至少有1人成績是“優秀”的概率；
(2)從前文所指的這10人（成績見莖葉圖）中隨機選取3人，記
表示測試成績為“優秀”的學生人數，求
的分布列及期望.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某產品的三個質量指標分別為x, y, z, 用綜合指標S =" x" + y + z評價該產品的等級. 若S≤4, 則該產品為一等品. 現從一批該產品中, 隨機抽取10件產品作為樣本, 其質量指標列表如下:
產品編號 | A1 | A2 | A3 | A4 | A5 |
質量指標(x, y, z) | (1,1,2) | (2,1,1) | (2,2,2) | (1,1,1) | (1,2,1) |
產品編號 | A6 | A7 | A8 | A9 | A10 |
質量指標(x, y, z) | (1,2,2) | (2,1,1) | (2,2,1) | (1,1,1) | (2,1,2) |
(Ⅰ) 利用上表提供的樣本數據估計該批產品的一等品率;
(Ⅱ) 在該樣品的一等品中, 隨機抽取兩件產品,
(1) 用產品編號列出所有可能的結果;
(2) 設事件B為 “在取出的2件產品中, 每件產品的綜合指標S都等于4”, 求事件B發生的概率.
查看答案和解析>>
科目：高中數學 來源： 題型：
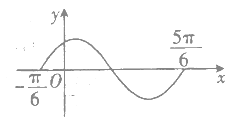
【題目】如圖所示的是函數
（
，
）在區間
上的圖象，將該函數圖象各點的橫坐標縮小到原來的一半（縱坐標不變），再向右平移
（
）個單位長度后，所得到的圖象關于直線
對稱，則的最小值為（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】目前共享單車基本覆蓋饒城市區，根據統計，市區所有人騎行過共享單車的人數已占
，騎行過共享單車的人數中，有
是學生（含大中專、高職及中學生），若市區人口按40萬計算，學生人數約為9.6萬．
（1）任選出一名學生，求他（她）騎行過共享單車的概率；
（2）隨著單車投放數量增加，亂停亂放成為城市管理的問題，如表是本市某組織累計投放單車數量
與亂停亂放單車數量
之間關系圖表：
累計投放單車數量 | 100000 | 120000 | 150000 | 200000 | 230000 |
亂停亂放單車數量 | 1400 | 1700 | 2300 | 3000 | 3600 |
計算關于的線性回歸方程（其中
精確到
，
值保留三位有效數字），并預測當
時，單車亂停亂放的數量；
（3）已知信州區、廣豐區、上饒縣、經開區四區中，其中有兩個區的單車亂停亂放數量超過標準，在“大美上饒”活動中，檢查組隨機抽取兩個區調查單車亂停亂放數量，
表示“單車亂停亂放數量超過標準的區的個數”，求的分布列和數學期望．
參考公式和數據：回歸直線方程
中的斜率和截距的最小二乘估計分別為
，
，
，
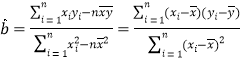查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】從某小區抽取50戶居民進行月用電量調查，發現其用電量都在50到350度之間，將用電量的數據繪制成頻率分布直方圖如下.
（1）求頻率分布直方圖中
的值并估計這50戶用戶的平均用電量；
（2）若將用電量在區間
內的用戶記為
類用戶，標記為低用電家庭，用電量在區間
內的用戶記為
類用戶，標記為高用電家庭，現對這兩類用戶進行問卷調查，讓其對供電服務進行打分，打分情況見莖葉圖：
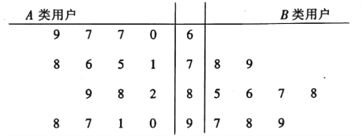
①從
類用戶中任意抽取3戶，求恰好有2戶打分超過85分的概率；
②若打分超過85分視為滿意，沒超過85分視為不滿意，請填寫下面列聯表，并根據列聯表判斷是否有
的把握認為“滿意度與用電量高低有關”？
滿意 | 不滿意 | 合計 | |
| |||
| |||
合計 |
附表及公式：
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
， 
.
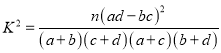查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
