
【題目】某產品的三個質量指標分別為x, y, z, 用綜合指標S =" x" + y + z評價該產品的等級. 若S≤4, 則該產品為一等品. 現從一批該產品中, 隨機抽取10件產品作為樣本, 其質量指標列表如下:
產品編號 | A1 | A2 | A3 | A4 | A5 |
質量指標(x, y, z) | (1,1,2) | (2,1,1) | (2,2,2) | (1,1,1) | (1,2,1) |
產品編號 | A6 | A7 | A8 | A9 | A10 |
質量指標(x, y, z) | (1,2,2) | (2,1,1) | (2,2,1) | (1,1,1) | (2,1,2) |
(Ⅰ) 利用上表提供的樣本數據估計該批產品的一等品率;
(Ⅱ) 在該樣品的一等品中, 隨機抽取兩件產品,
(1) 用產品編號列出所有可能的結果;
(2) 設事件B為 “在取出的2件產品中, 每件產品的綜合指標S都等于4”, 求事件B發生的概率.
【答案】(Ⅰ) 0.6 (Ⅱ) (1) 15種(2)![]()
【解析】
試題(1)首先將3項指標相加,求出綜合指標S.然后找出其中![]() 的產品,便可估計出該批產品的一等品率.(2)(1)根據(1)題結果可知,
的產品,便可估計出該批產品的一等品率.(2)(1)根據(1)題結果可知,![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 為一等品,共6件.從這6件一等品中隨機抽取2件產品的所有可能結果為:
為一等品,共6件.從這6件一等品中隨機抽取2件產品的所有可能結果為:![]() ,
,![]() ,
,![]() ,
,![]() ,共15種.(2)在該樣本的一等品中,綜合指標S等于4的產品編號分別為
,共15種.(2)在該樣本的一等品中,綜合指標S等于4的產品編號分別為![]() 、
、![]() 、
、![]() 、
、![]() ,則事件B發生的所有可能結果為
,則事件B發生的所有可能結果為![]() 共6種.由古典概型概率公式可得事件B發生的概率.
共6種.由古典概型概率公式可得事件B發生的概率.
試題解析:(1)10件產品的綜合指標S如下表所示:
產品編號 |
|
|
|
|
|
|
|
|
|
|
S | 4 | 4 | 6 | 3 | 4 | 5 | 4 | 5 | 3 | 5 |
其中![]() 的有
的有![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,共6件,故該樣本的一等品率為
,共6件,故該樣本的一等品率為![]() ,從而可估計該批產品的一等品率為
,從而可估計該批產品的一等品率為![]() .
.
(2)(1)在該樣本的一等品中,隨機抽取2件產品的所有可能結果為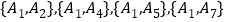 ,
,![]() ,
,![]() ,共15種.(2)在該樣本的一等品中,綜合指標S等于4的產品編號分別為
,共15種.(2)在該樣本的一等品中,綜合指標S等于4的產品編號分別為![]() 、
、![]() 、
、![]() 、
、![]() ,則事件B發生的所有可能結果為
,則事件B發生的所有可能結果為![]() 共6種.所以
共6種.所以![]() .
.


科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為![]() (其中
(其中![]() 為參數),以原點
為參數),以原點![]() 為極點,
為極點,![]() 軸正半軸為極軸建立極坐標系,曲線
軸正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() (
(![]() 為常數,
為常數,![]() ,且
,且![]() ),點
),點![]() (
(![]() 在
在![]() 軸下方)是曲線
軸下方)是曲線![]() 與
與![]() 的兩個不同交點.
的兩個不同交點.
(1)求曲線![]() 的普通方程和
的普通方程和![]() 的直角坐標方程;
的直角坐標方程;
(2)求![]() 的最大值及此時點
的最大值及此時點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,游客從景點![]() 下山至
下山至![]() 有兩種路徑:一種是從
有兩種路徑:一種是從![]() 沿直線步行到
沿直線步行到![]() ,另一種是先從
,另一種是先從![]() 乘纜車到
乘纜車到![]() ,然后從
,然后從![]() 沿直線步行到
沿直線步行到![]() .現有甲、乙兩位游客從
.現有甲、乙兩位游客從![]() 下山,甲沿
下山,甲沿![]() 勻速步行,速度為
勻速步行,速度為![]() 米/分鐘.在甲出發
米/分鐘.在甲出發![]() 分鐘后,乙從
分鐘后,乙從![]() 乘纜車到
乘纜車到![]() ,在
,在![]() 處停留
處停留![]() 分鐘后,再從
分鐘后,再從![]() 勻速步行到
勻速步行到![]() .已知纜車從
.已知纜車從![]() 到
到![]() 要
要![]() 分鐘,
分鐘,![]() 長為
長為![]() 米,若
米,若![]() ,
,![]() .為使兩位游客在
.為使兩位游客在![]() 處互相等待的時間不超過
處互相等待的時間不超過![]() 分鐘,則乙步行的速度
分鐘,則乙步行的速度![]() (米/分鐘)的取值范圍是 __________.
(米/分鐘)的取值范圍是 __________.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 是定義在R上的奇函數,其中
是定義在R上的奇函數,其中![]() 為指數函數,且
為指數函數,且![]() 的圖象過定點
的圖象過定點![]() .
.
(1)求函數![]() 的解析式;
的解析式;
(2)若關于x的方程,![]() 有解,求實數a的取值范圍;
有解,求實數a的取值范圍;
(3)若對任意的![]() ,不等式
,不等式![]() 恒成立,求實數k的取值范圍.
恒成立,求實數k的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為響應綠色出行,某市在推出“共享單車”后,又推出“新能源租賃汽車”.每次租車收費的標準由兩部分組成:①里程計費:1元/公里;②時間計費:![]() 元/分.已知陳先生的家離上班公司
元/分.已知陳先生的家離上班公司![]() 公里,每天上、下班租用該款汽車各一次.一次路上開車所用的時間記為
公里,每天上、下班租用該款汽車各一次.一次路上開車所用的時間記為![]() (分),現統計了50次路上開車所用時間,在各時間段內頻數分布情況如下表所示
(分),現統計了50次路上開車所用時間,在各時間段內頻數分布情況如下表所示

將各時間段發生的頻率視為概率,一次路上開車所用的時間視為用車時間,范圍為![]()
![]() 分.
分.
(1)估計陳先生一次租用新能源租賃汽車所用的時間不低于![]() 分鐘的概率;
分鐘的概率;
(2)若公司每月發放![]() 元的交通補助費用,請估計是否足夠讓陳先生一個月上下班租用新能源租賃汽車(每月按
元的交通補助費用,請估計是否足夠讓陳先生一個月上下班租用新能源租賃汽車(每月按![]() 天計算),并說明理由.(同一時段,用該區間的中點值作代表)
天計算),并說明理由.(同一時段,用該區間的中點值作代表)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在平面直角坐標系![]() 中,以
中,以![]() 軸為始邊做兩個銳角
軸為始邊做兩個銳角![]() ,它們的終邊分別與單位圓相交于A,B兩點,已知A,B的橫坐標分別為
,它們的終邊分別與單位圓相交于A,B兩點,已知A,B的橫坐標分別為![]()

(1)求![]() 的值; (2)求
的值; (2)求![]() 的值。
的值。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為提升教師專業功底,引領青年教師成長,某市教育局舉行了全市“園丁杯”課堂教學比賽,在這次比賽中,通過采用錄像課評比的片區預賽,有![]() 共10位選手脫穎而出進入全市決賽.決賽采用現場上課形式,從學科評委庫中采用隨機抽樣抽選代號1,2,3,…,7的7名評委,規則是:選手上完課,評委們當初評分,并從7位評委評分中去掉一個最高分,去掉一個最低分,根據剩余5位評委的評分,算出平均分作為該選手的最終得分.記評委
共10位選手脫穎而出進入全市決賽.決賽采用現場上課形式,從學科評委庫中采用隨機抽樣抽選代號1,2,3,…,7的7名評委,規則是:選手上完課,評委們當初評分,并從7位評委評分中去掉一個最高分,去掉一個最低分,根據剩余5位評委的評分,算出平均分作為該選手的最終得分.記評委![]() 對某選手評分排名與該選手最終排名的差的絕對值為“評委
對某選手評分排名與該選手最終排名的差的絕對值為“評委![]() 對這位選手的分數排名偏差”
對這位選手的分數排名偏差”![]() .排名規則:由高到低依次排名,如果選手分數一樣,認定名次并列(如:選手
.排名規則:由高到低依次排名,如果選手分數一樣,認定名次并列(如:選手![]() 分數一致排在第二,則認為他們同屬第二名,沒有第三名,接下來分數為第四名).七位評委評分情況如下表所示:
分數一致排在第二,則認為他們同屬第二名,沒有第三名,接下來分數為第四名).七位評委評分情況如下表所示:
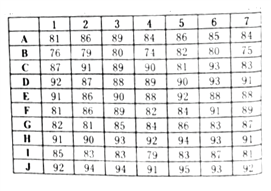
(1)根據最終評分表,填充如下表格:

(2)試借助評委評分分析表,根據評委對各選手的排名偏差的平方和,判斷評委4與評委5在這次活動中誰評判更準確.
____號評委評分分析表
選手 | A | B | C | D | E | F | G | H | I | J |
最終排名 | ||||||||||
評分排名 | ||||||||||
排名偏差 |
(3)從這10位選手中任意選出3位,記其中評委4比評委5對選手排名偏差小的選手數位![]() ,求隨機變量
,求隨機變量![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】經觀測,某公路段在某時段內的車流量![]() (千輛/小時)與汽車的平均速度
(千輛/小時)與汽車的平均速度![]() (千米/小時)之間有函數關系:
(千米/小時)之間有函數關系:![]() .
.
(1)在該時段內,當汽車的平均速度![]() 為多少時車流量
為多少時車流量![]() 最大?最大車流量為多少?(精確到0.01)
最大?最大車流量為多少?(精確到0.01)
(2)為保證在該時段內車流量至少為10千輛/小時,則汽車的平均速度應控制在什么范圍內?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com